题目内容
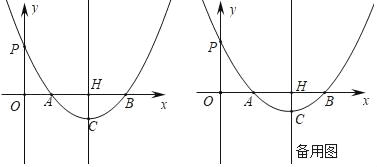
【题目】如图，在平面直角坐标系中，二次函数y＝a（x﹣1）（x﹣5）（a＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于P点，过其顶点C作直线CH⊥x轴于点H．
（1）若∠APB＝30°，请直接写出满足条件的点P的坐标；
（2）当∠APB最大时，请求出a的值；
（3）点P、O、C、B能否在同一个圆上？若能，请求出a的值，若不能，请说明理由．
（4）若a＝
，在对称轴HC上是否存在一点Q，使∠AQP＝∠ABP？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
【答案】（1）点P坐标为（0，
）或（0，
）；（2）
；（3）能，a的值为
；（4）点Q坐标为（3，3+
）或（3，3﹣）．
【解析】
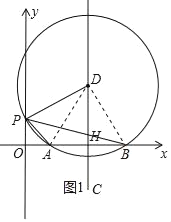
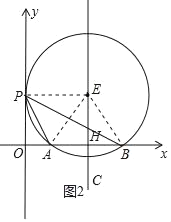
（1）作△PAB的外接圆⊙D，连接DP、DA、DB，证△ABD是等边三角形，求A（1，0），B（5，0），得DP＝DA＝AB＝4，H（3，0），得直线CH：x＝3，求出D（3，2
）
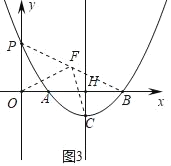
设P（0，p）（p＞0），由PD2＝32+（2﹣p）2＝42，求出P的坐标；（2）作△PAB的外接圆⊙E，连接EP、EA、EB，如图2，由切线性质，得四边形OHEP是矩形，在Rt△AEH中，EH＝
，求出0P得点P坐标为（0，
），代入抛物线解析式可得；（3）连接PB，取PB中点F，连接FO、FC，证点P、O、B在以点F为圆心、FB的长为半径的圆上，若点C在⊙F上，则FC＝FB，由抛物线解析式y＝a（x﹣1）（x﹣5）＝ax2﹣6ax+5a＝a（x﹣3）2﹣4a，得P（0，5a），C（3，﹣4a），再求F坐标，由
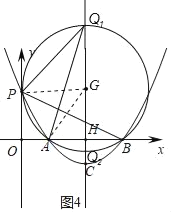
，得
，解方程可得；（4）作△PAB的外接圆⊙G，连接GP、GA，设⊙G与直线CH交于点Q，得∠AQP＝∠ABP，当a＝
时，点P（0，1），设G（3，b）（b＞0），由GP＝GA，得32+（b﹣1）2＝（3﹣1）2+b2，进一步得G（3，3），GQ＝GA＝
，可得点Q坐标有两种可能．
解：（1）作△PAB的外接圆⊙D，连接DP、DA、DB，如图1
∴DP＝DA＝DB，
∵C为抛物线顶点且CH⊥x轴
∴CH为抛物线对称轴，即CH垂直平分AB
∴D在直线CH上
∵∠APB＝30°
∴∠ADB＝2APB＝60°
∴△ABD是等边三角形
∵当y＝0时，a（x﹣1）（x﹣5）＝0 解得：x1＝1，x2＝5
∴A（1，0），B（5，0）
∴DP＝DA＝AB＝4，H（3，0），直线CH：x＝3
∴AH＝2，DH＝AH＝2
∴D（3，2）
设P（0，p）（p＞0）
∴PD2＝32+（2﹣p）2＝42
解得：p1＝，p2＝
∴点P坐标为（0，）或（0，）
（2）作△PAB的外接圆⊙E，连接EP、EA、EB，如图2
∵∠AEB＝2∠APB
∴∠AEB最大时，∠APB最大
∵AB＝4是定值
∴EH最小时，∠AEB最大，此时⊙E与y轴相切于点P
∴EP⊥y轴于P
∴四边形OHEP是矩形
∴PE＝OH＝3
∴EA＝PE＝3
∴Rt△AEH中，EH＝
∴OP＝EH＝
∴点P坐标为（0，），代入抛物线解析式得：5a＝
∴a＝
（3）点P、O、C、B能在同一个圆上．
连接PB，取PB中点F，连接FO、FC
∵∠POB＝90°
∴OF＝PF＝FB＝
PB
∴点P、O、B在以点F为圆心、FB的长为半径的圆上
若点C在⊙F上，则FC＝FB
∵抛物线解析式y＝a（x﹣1）（x﹣5）＝ax2﹣6ax+5a＝a（x﹣3）2﹣4a
∴P（0，5a），C（3，﹣4a）
∵B（5，0），F为PB中点
∴F
∴
∴
解得：a1＝，a2＝﹣（舍去）
∴a的值为
（4）对称轴HC上存在一点Q，使∠AQP＝∠ABP
作△PAB的外接圆⊙G，连接GP、GA，设⊙G与直线CH交于点Q
∴∠AQP＝∠ABP
当a＝时，点P（0，1）
设G（3，b）（b＞0）
∴GP2＝32+（b﹣1）2，GA2＝（3﹣1）2+b2
∵GP＝GA
∴32+（b﹣1）2＝（3﹣1）2+b2
解得：b＝3
∴G（3，3），GQ＝GA＝
∴点Q坐标为（3，3+ ）或（3，3﹣）．
