题目内容
4．已知抛物线y=x2-x-2与x轴的一个交点为（m，0），则代数式m2-m+2016的值为（ ）| A． | 2017 | B． | 2018 | C． | 2019 | D． | 2020 |
分析 直接利用抛物线上点的坐标性质进而得出m2-m=2，即可得出答案．
解答 解：∵抛物线y=x2-x-2与x轴的一个交点为（m，0），
∴m2-m-2=0，
∴m2-m=2，
∴m2-m+2016=2+2016=2018．
故选：B．
点评 此题主要考查了抛物线与x轴的交点，正确得出关于m的代数式的值是解题关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
14．某商品的原价是每件x元，在销售时每件加价20元，再降价15%，则现在每件的售价是（ ）元．
| A． | 15%x+20 | B． | （1-15%）x+20 | C． | 15%（x+20） | D． | （1-15%）（x+20） |
15．用配方法解一元二次方程x2+6x-3=0，原方程可变形为（ ）
| A． | （x+3）2=3 | B． | （x+3）2=6 | C． | （x+3）2=12 | D． | （x+3）2=9 |
12．下面各种说法中正确的是（ ）
| A． | 两数的差一定小于被减数 | |
| B． | 两数的和一定大于每一个加数 | |
| C． | 两数的绝对值相等，这两个数也一定相等 | |
| D． | 两数的积不一定比每一个因数大 |
19．
如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（ ）
如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（ ）| A． | BD=CD | B． | AB=AC | C． | ∠B=∠C | D． | ∠BDA=∠CDA |
9．下列说法中正确的是（ ）
| A． | 近似数11.30是精确到个位的数 | |
| B． | 近似数41.3是精确到十分位的数 | |
| C． | 近似数五百和近似数500的精确度是相同的 | |
| D． | 近似数1.7和1.70是一样的 |
4．
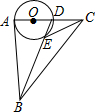如图，△ABC中，∠BAC=90°，AB=AC=2，D为AC上一动点，以AD为直径的⊙O交BD于E，则线段CE的最小值为（ ）
如图，△ABC中，∠BAC=90°，AB=AC=2，D为AC上一动点，以AD为直径的⊙O交BD于E，则线段CE的最小值为（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{5}$+1 | C． | 2$\sqrt{5}$ | D． | $\sqrt{5}$-1 |
1．下列条件中，不能判断两个三角形全等的方法有（ ）
| A． | 两边和一个角分别相等的两个三角形 | |
| B． | 两个角及其夹边分别相等的两个三角形 | |
| C． | 三边分别相等的两个三角形 | |
| D． | 斜边和一条直角边分别相等的两个直角三角形 |
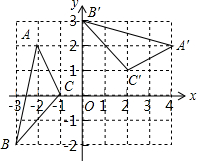如图，在平面直角坐标系xOy中，每个小方格的边长为1，将△ABC绕点P旋转得到△A′B′C′，则点P的坐标为（1，-1）．