题目内容
12.已知数轴上有A、B两点,A、B之间的距离为a,点A与原点O的距离为b(b>a),则所有满足条件的点B与原点O的距离的和为( )| A. | 2a+2b | B. | 2b-2a | C. | 2b | D. | 4b |
分析 先用b表示出A点表示的数,再由A,B两点之间的距离为a可得出B点表示的数,进而可得出结论.
解答 解:∵点A与原点O的距离为b,
∴点A表示数b或-b.
∵A,B两点之间的距离为a,
∴当点A表示b时,|B-b|=a,解得B=a+b或B=b-a;
当点A表示-b时,|B+b|=a,解得B=a-b或B=-a-b,
∴所有满足条件的B与原点O的距离=a+b+|b-a|+|a-b|+|-a-b|
=2a+2b+2|a-b|
=2a+2b+2(b-a)
=2a+2b+2b-2a
=4b.
故选:D.
点评 本题考查的是数轴,熟知数轴上两点间距离的定义是解答此题的关键.

练习册系列答案
相关题目
2.当$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{d}$=$\frac{d}{a}$时,$\frac{a-b+c-d}{a+b-c+d}$的值为( )
| A. | 0 | B. | -1 | C. | 2 | D. | 0或-2 |
3.若(3-a)x|a-2|+3=0是关于x的一元一次方程,则a的值为( )
| A. | 3 | B. | 1 | C. | 3或1 | D. | -3 |
4. 如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )
如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )
 如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )
如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )| A. | AB=asinα | B. | AB=$\frac{a}{cosα}$ | C. | AB=$\frac{a}{tanα}$ | D. | AB=a•tanα |
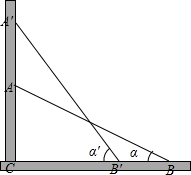 如图,一根3m长的竹竿AB斜靠在墙上,当端点A离地面的高度AC长为1m时,竹竿AB的倾斜角α的正切tanα的值是多少?当端点A位于A′,离地面的高度A′C为2m时,倾斜角α′的正切tanα′的值是多少?tanα的值可以大于100吗?
如图,一根3m长的竹竿AB斜靠在墙上,当端点A离地面的高度AC长为1m时,竹竿AB的倾斜角α的正切tanα的值是多少?当端点A位于A′,离地面的高度A′C为2m时,倾斜角α′的正切tanα′的值是多少?tanα的值可以大于100吗?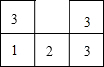 如图是从上面看由一些小正方体搭成的几何体的视图.正方形中的数字表示在该位置小正方体的个数.
如图是从上面看由一些小正方体搭成的几何体的视图.正方形中的数字表示在该位置小正方体的个数.