题目内容
19.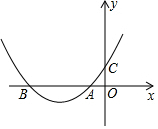 如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为A、B、C,且OA=OC=1,则下列关系中正确的是( )
如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为A、B、C,且OA=OC=1,则下列关系中正确的是( )| A. | a+b=-1 | B. | a-b=-1 | C. | b<2a | D. | ac<0 |
分析 先得到A(-1,0),C(0,1),再把A点和C点坐标代入抛物线解析式得到a-b+c=0,c=1,则可对A、B进行判断;利用抛物线开口方向得到a>0,利用抛物线与y轴的交点位置得到c>0,则可对D进行判断;利用对称轴的位置得到x=-$\frac{b}{2a}$<-1,则可对C进行判断.
解答 解:∵OA=OC=1,
∴A(-1,0),C(0,1),
把A(-1,0),C(0,1)代入y=ax2+bx+c得a-b+c=0,c=1,
∴a-b=-1,所以A选项错误,B选项正确;
∵抛物线开口向上,
∴a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴ac>0,所以D选项错误;
∵x=-$\frac{b}{2a}$<-1,
∴b>2a,所以C选项错误.
故选B.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数图象与系数的关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.运用乘法公式计算(x-2)2的结果是( )
| A. | x2-4x+4 | B. | x2-4 | C. | x2+4x+4 | D. | x2-2x+4 |
10. 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |
4.已知一组数据:1,2,6,3,3,下列说法错误的是( )
| A. | 众数是3 | B. | 中位数是6 | C. | 平均数是3 | D. | 方差是2.8 |
11. 随着移动互联网的快速发展,OFO、摩拜等互联网共享单车应运而生并快速发展.小冬骑的摩拜单车,爸爸骑的摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的函数关系的图象如图,根据图象分析,何时俩人相遇,谁先到( )
随着移动互联网的快速发展,OFO、摩拜等互联网共享单车应运而生并快速发展.小冬骑的摩拜单车,爸爸骑的摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的函数关系的图象如图,根据图象分析,何时俩人相遇,谁先到( )
 随着移动互联网的快速发展,OFO、摩拜等互联网共享单车应运而生并快速发展.小冬骑的摩拜单车,爸爸骑的摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的函数关系的图象如图,根据图象分析,何时俩人相遇,谁先到( )
随着移动互联网的快速发展,OFO、摩拜等互联网共享单车应运而生并快速发展.小冬骑的摩拜单车,爸爸骑的摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的函数关系的图象如图,根据图象分析,何时俩人相遇,谁先到( )| A. | 4分钟时相遇,爸爸先到 | B. | 20分钟时相遇,爸爸先到 | ||
| C. | 4分时相遇,小冬先到 | D. | 20分钟时相遇,小冬先到 |
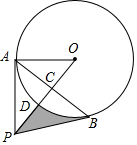 如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.
如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.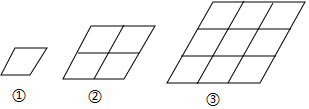
 某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.