题目内容
17.已知一次函数y=kx+b的图象经过点A(-1,3)和点B(2,-3).(1)求这个一次函数的表达式;
(2)求直线AB与坐标轴所围成的三角形的面积;
(3)将该函数的图象向右平移6个单位,求平移后的图象与x轴的交点的坐标.
分析 (1)把A、B两点代入可求得k、b的值,可得到一次函数的表达式;
(2)分别令y=0、x=0可求得直线与两坐标轴的两交点坐标,可求得所围成的三角形的面积;
(3)根据左加右减的法则可得到平移后的函数表达式,再令y=0,求出x的值,即可求解.
解答 解:(1)∵一次函数y=kx+b的图象经过点A(-1,3)和点B(2,-3),
∴$\left\{\begin{array}{l}{-k+b=3}\\{2k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=1}\end{array}\right.$,
∴一次函数为y=-2x+1;
(2)在y=-2x+1中,分别令x=0、y=0,
可求得一次函数与两坐标轴的交点坐标分别为(0,1)、($\frac{1}{2}$,0),
所以直线与两坐标轴围成的三角形的面积为:S=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$;
(3)函数y=-2x+1向右平移6个单位,则可得平移后的函数为y=-2(x-6)+1,即y=-2x+13,
令y=0,得x=$\frac{13}{2}$,
所以平移后的图象与x轴的交点的坐标为($\frac{13}{2}$,0).
点评 本题主要考查待定系数法求函数解析式,掌握待定系数法的应用关键是点的坐标,即把点坐标代入得到关于系数的方程组,求解即可.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 如图,在雷达探测区内,可以建立平面直角坐标系表示位置,当我方两架飞机在A(-1,2)与B(3,2)位置,可疑飞机在(-1,3)位置,你能找到这个直角坐标系的横,纵坐标轴的位置吗?把它们表示出来,并确定可疑飞机的所处方位.
如图,在雷达探测区内,可以建立平面直角坐标系表示位置,当我方两架飞机在A(-1,2)与B(3,2)位置,可疑飞机在(-1,3)位置,你能找到这个直角坐标系的横,纵坐标轴的位置吗?把它们表示出来,并确定可疑飞机的所处方位.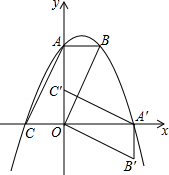 已知抛物线y=-$\frac{1}{2}$x2+bx+4的对称轴为x=1,与y交于点A,与x轴负半轴交于点C,作平行四边形ABOC并将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′O′C′.
已知抛物线y=-$\frac{1}{2}$x2+bx+4的对称轴为x=1,与y交于点A,与x轴负半轴交于点C,作平行四边形ABOC并将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′O′C′.