��Ŀ����
����ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
���й���x�ķ����У�һ����һԪ���η��̵��ǣ�������
A. ��m��3��x2��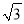 x��2 B. k2x+5k+6=0; C.
x��2 B. k2x+5k+6=0; C.  x2��
x2�� x��
x�� =0; D. 3x2+
=0; D. 3x2+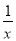 ��2=0
��2=0
������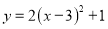 �Ķ��������ǣ� ��
�Ķ��������ǣ� ��
A. ��3, 1�� B. ��3��-1) C. (-3, 1) D. (-3, -1)
�鿴�������з���
(1)��x+1��2��9=0
(2)��x��1��3=8��
�鿴���������ܰ�һ��������ֱ����������취����˵�����еĵ�����
�鿴��С����С�������ۡ����ʱΪʲôǹ����Ҫ�ǣ���
С��������������ֻ��һ��ֱ�ߣ�����ǹ����Ҫ���ǣ�
С�����������ۿ���һ�㣬�ǿ���һ�㣬Ŀ�꿴��һ�㣬�ⲻ�����������𣿶���һ����ѽ��
����˵˵��Ĺ۵㣮
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
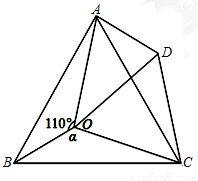
��ͼ����O�ǵȱߡ�ABC��һ�㣬��AOB=110�㣬��BOC=��������BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC������OD��
��1����֤����COD�ǵȱ������Σ�
��2������=150��ʱ�����жϡ�AOD����״����˵�����ɣ�
һ�κ���y=kx+b��ͼ���뷴��������y=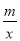 ��ͼ���ڵ�A��2��1����B����1��n������.
��ͼ���ڵ�A��2��1����B����1��n������.
��1�����������Ľ���ʽ��
��2����һ���������Ľ���ʽ��
��3�����AOB�����.
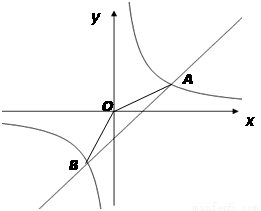
��ͼ��ʾ�� ��һ�������ش�10m �ߵĴ�A����ˮ��������ˮ�������ˮ��������״����������ߵ���ߵ�M ��ǽ1m�������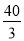 m.
m.
��1���������ߵĽ���ʽ��
��2����ˮ����ص�B��ǽ�ľ���OB.
��ͼ��ʾ��AB�ǡ�O��ֱ����BD�ǡ�O���ң��ӳ�BD����C��ʹDC=BD������AC������D��DE��AC��E��
��1����֤��AB=AC��
��2����֤��DEΪ��O�����ߣ�
�̵�ֻ��ѩ�̡����֡���֭����֭�������ϣ�ÿ�������������㣬ijͬѧȥ�õ깺�����ϣ�ÿ�����ϱ�ѡ�еĿ�������ͬ��
��1������ȥ��һƿ���ϣ���������֭�ĸ����� ��
��2����������ȥ�����ϣ�ÿ����һƿ����������������Ʒ�ֲ�ͬ��������״ͼ���б��������ǡ����ѩ�̺���֭�ĸ��ʣ�
�鿴����֪�����߾�������A(2,6)��B(-1,0)��C(3,0)��
����������������Ӧ�Ķ��κ����Ľ���ʽ��
��2��д�����ĶԳ���Ͷ�������.
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ���ڡ�ABC�У���B=��C��ADΪ��ABC�����ߣ���ô���н��۴�����ǣ�������
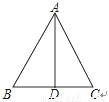
A. ��ABD�ա�ACD B. ADΪ��ABC�ĸ��� C. ADΪ��ABC�Ľ�ƽ���� D. ��ABC�ǵȱ�������
D ������������������ߡ�B=��C�� ��AB=AC�� ��AD�ǡ�ABC�����ߣ� ��AD��BC����BAD=��CAD����AD�ǡ�ABC�ĸߣ�ADΪ��ABC�Ľ�ƽ���ߣ� ���ADB=��ADC=90�㣬 �ڡ�ABD�͡�ACD�� ���ABD�ա�ACD�� ��ѡ��A��B��C����ȷ�� ������ֻ֪���Ƴ�AC=AB�������Ƴ�AC��AB��BC�Ĺ�ϵ�� �����ܵ�...��������������������ǣ�������
A. ȷ�����¼������ĸ���Ϊ1��
B. ƽ���ҵ�ֱ����ֱ���ң�
C. ��n���ζ�����Գ�ͼ��,������n���Գ��
D. ������һ�ߵĶԽǶ�Ӧ��ȵ�����������ȫ�ȡ�
�鿴����a��b��c�������ε����ߣ����в��ܹ���ֱ�������ε��ǣ�������
A. a2=��b+c����b��c�� B. a��b��c=1��  ��2
��2
C. a=32��b=42��c=52 D. a=5��b=12��c=13
�鿴����ͼ���������������У���AB=AC�����ܱ�һ��ֱ�߷ֳ�����С���������ε��ǣ� ��
A. ��1����2����3�� B. ��1����3����4�� C. ��2����3����4�� D. ��1����2����4��
�鿴����ͼ��PB��AB��B��PC��AC��C����PB=PC�����APB�ա�APC�������ǣ�������
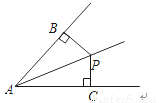
A. SAS B. ASA C. HL D. AAS
�鿴����ͼ���ڡ�ABC�У�AB��AC��5��P��BC���ϳ�B��C���������һ�㣬�����ʽAP2��PB��PC���� (����)
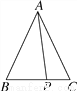
A. 25 B. 15 C. 20 D. 30
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
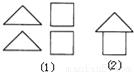
��ƴͼ��Ϸ�У���ͼ��1��������ֽƬ�У���ȡ����ֽƬ����ƴ�ɡ����ӡ���ͼ��2���ĸ���Ϊ������
��֪�����ĵױ߳�������ǡ���Ƿ���x2-6x+8��0������������������ε��ܳ�Ϊ_________
�鿴����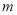 =_______ʱ������
=_______ʱ������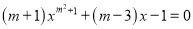 ��һԪ���η���.
��һԪ���η���.
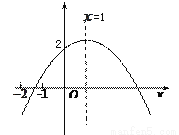
��ͼ��ʾ�����κ���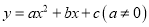 ��ͼ��ĶԳ�����ֱ��x=1���Ҿ����㣨0,2���������н��ۣ���ac��0����
��ͼ��ĶԳ�����ֱ��x=1���Ҿ����㣨0,2���������н��ۣ���ac��0����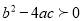 ����a+c��2-b����
����a+c��2-b����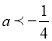 �� ��x=-5��x=7ʱ����ֵ��ȣ�������ȷ�Ľ����� �� ��
�� ��x=-5��x=7ʱ����ֵ��ȣ�������ȷ�Ľ����� �� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴����2016�����У��ө�3����1�� 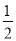 ��1��3��������У������ȡһ��������Ϊa������aʹ����x�IJ���ʽ��
��1��3��������У������ȡһ��������Ϊa������aʹ����x�IJ���ʽ�� �⣬��ʹ����x�ķ�ʽ����
�⣬��ʹ����x�ķ�ʽ����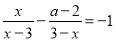 �������⣬��ô��5��������������������a��ֵ֮���ǣ�������
�������⣬��ô��5��������������������a��ֵ֮���ǣ�������
A. ��3 B. ��2 C. ��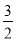 D.
D. 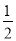
��ͼ��ԲO����AB��ֱƽ�ְ뾶OC�����ı���OACBһ���ǣ�������
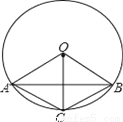
A. ������ B. ������ C. ���� D. ����
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ����AOB��90�㣬��B��30�㣬��A��OB�����Կ������ɡ�AOB�Ƶ�O˳ʱ����ת
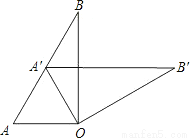
A. 30�� B. 45�� C. 60�� D. 90��
C ������������������ߡ�AOB=90�㣬��B=30�㣬 ���A=60�㣮 �ߡ�A��OB����Կ������ɡ�AOB�Ƶ�O˳ʱ����ת���Ƕȵõ��ģ� ��OA=OA�䣮 ���OAA���ǵȱ������Σ� ���AOA��=60�㣬����ת�Ǧ��Ĵ�С������60�㣮 ��ѡC.��֪a��0����ͬһֱ������ϵ�У�����y=ax��y=ax2��ͼ���п����ǣ�������
A. 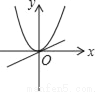 B.
B. 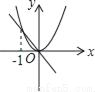 C.
C. 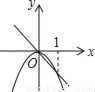 D.
D. 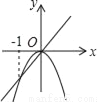
��ͼ��ԲO�ǡ�ABC�����Բ����A=68�㣬���BOC�Ĵ�С�ǣ�������
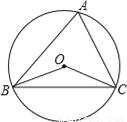
A. 22�� B. 32�� C. 136�� D. 68��
�鿴�����䷽���ⷽ��x2+6x+4=0�����б�����ȷ���ǣ�������
A. ��x+3��2=��4 B. ��x��3��2=4 C. ��x+3��2=5 D. ��x+3��2=��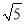
�����¼��У����ڱ�Ȼ�¼����ǣ� ��
A�����κ�����ͼ����������
B������һ��һԪ���η��̶���ʵ����
C�������ε������������ε��ⲿ
D��Ͷ��һö���ȵ�Ӳ��100�Σ����泯�ϵĴ���Ϊ50��
�鿴������ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
С����С�������ۡ����ʱΪʲôǹ����Ҫ�ǣ���
С��������������ֻ��һ��ֱ�ߣ�����ǹ����Ҫ���ǣ�
С�����������ۿ���һ�㣬�ǿ���һ�㣬Ŀ�꿴��һ�㣬�ⲻ�����������𣿶���һ����ѽ��
����˵˵��Ĺ۵㣮
����ȷ��һ��ֱ�� ������������������������ֱ�ߵ���������ȷ��һ��ֱ�߽��н�ɣ� ����������������ۿ���һ�㣬�ǿ���һ�㣬Ŀ�꿴��һ�㣬��ôҪ������Ŀ�꣬������Ŀ��ȷ��������ֱ�ߣ�Ӧ���ӵ����ߵ�ֱ���غϣ������Ǻ�Ŀ����ȷ��������ֱ���غϣ����ﵽ�����Ĵ��Ķ��� ���仰˵Ҫ������Ŀ��ͱ���ʹ����������Ŀ����ȷ����ֱ���ϣ���������ԲȦ�ֱ��ʾ�������Ϻ��������ϣ�����������ԲȦ�ڸ����������������������������ڸ��������ڣ��������������ڣ���������Ӧ�����������˵��������ԲȦ���ص����ֱ�ʾʲô���ļ�����

��֪x+12ƽ�����ǡ�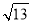 ��2x+y��6����������2����3xy������ƽ������
��2x+y��6����������2����3xy������ƽ������
��֪��|a��1|+|b+2|=0����2a+b��ֵ��
�鿴����ͼ��һ�����������ĵ���߳�Ϊ2cm����Ϊ4cm��
��1������������ж��ٸ��棿�������IJ������
��2������������ж��ٸ����㣿�ж������⣿
��3�����ú��� �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ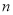 �����Ķ������������������������
�����Ķ������������������������
�ڵ�ʽ������������ǡ�����x2��y2+8y��4=x2����___________����
�鿴�� ��������- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�������ڡ�ABC�У�AC��BC��2����C��90�㣬��һ����������ΰ��ֱ�Ƕ������б��AB���е�P���������ǰ��Ƶ�P��ת�����ǰ����ֱ�DZ߷ֱ�����AC��CB��D��E���㡣ͼ�٣��ڣ�������ת���ǰ�õ���ͼ���е�3��������о���
��1�����ǰ�ABC�Ƶ�P��ת���۲��߶�PD��PE֮����ʲô������ϵ�������ͼ�ڼ���֤����
��2�����ǰ�ABC�Ƶ�P��ת����PBE�Ƿ���Ϊ���������Σ����ܣ�ָ�������������д����PBEΪ����������ʱCE�ij����������ܣ���˵�����ɡ���ͼ�ܲ��ã�
ijó��˾���������ࡱ���ݴ�ײˣ�����Ϊÿ��20Ԫ����۲��Ź涨�����۵���ÿ�ò��ó���80Ԫ��Ҳ���õ���30Ԫ�������鷢�֣��վ�������y���ã������۵���x��Ԫ/�ã�����һ�κ�����ϵ������ÿ���ۼ�60Ԫʱ���վ�����90�ã�ÿ���ۼ�30Ԫʱ���վ�����120�ã�
��1�����վ�������y�����۵���x�ĺ�����ϵʽ��
��2�������۹����У�ÿ�컹Ҫ֧����������200Ԫ������������w��Ԫ�������۵���x֮��ĺ�����ϵʽ���������۵���Ϊ��ֵʱ���ɻ��������������������������Ƕ��٣�
�鿴��ij��˾��ƺ�Ļ�������50����״��ͬ����������ɵģ�Ϊ�ι������ÿ�λ����谴���0.4m���費��ֹܣ���ͼ������������Ϊ�˼������費��ֹ��������ܳ��ȣ������Ա�����ͼ��ʾ�����ݣ�
��1����������ߵĽ���ʽ��
��2���������費��ֹܵ��ܳ��ȣ�
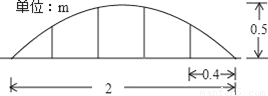
ij�����û�������ij�ֻ��磬����ʵ�鷢��ÿ���ӯ����ÿ�����������һ���Ĺ�ϵ��ÿ��ֲ��3��ʱ��ƽ������ӯ��3Ԫ����ͬ����������������ÿ������1�꣬ƽ������ӯ���ͼ���0.5Ԫ��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ�����ꣿ
�鿴����ͼ��������ABCD��������A1B1C1D1����ij�����ĶԳƣ���֪A, D1,D���������ֱ��ǣ�0,4������0��3������0��2��.
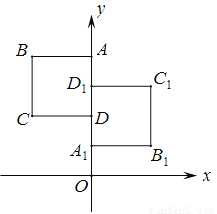
(1)�Գ����ĵ����ꣻ
(2)�����B, C, B1 , C1������.
�鿴��ʵ���������һ��أ������һ��ͼ������һ��������תһ���ǶȦ�����С��360�㣩���ܹ���ԭ����ͼ���غϣ���ô���ͼ�ν�����ת�Գ�ͼ�Σ�������������ת�Գ����ģ������������ת�Գ�ͼ�ε�һ����ת�ǣ�����������涨����������⣺
��1����д��һ����һ����ת����90����ת�Գ�ͼ�Σ����ͼ�ο�����_____��
��2���߹���ͼ����ͼ�еĵȱ��������ڲ�����һ��ͼ�Σ�ʹ������ͼ�κ�����ȱ������ι��ɵ��������һ����ת�Գ�ͼ������һ����Գ�ͼ�Σ�������ͼ����ʵ�ߣ���ͼ���������ߣ������ۼ�����д��������
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
 ��ƽ������ �� ��
��ƽ������ �� ��
A. 4 B. 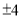 C.
C. 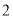 D.
D. 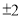
����������Ŀ�������̡�����Ĵ��š������Լ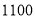 ������ң��ÿ�ѧ��������ʾ�� ����
������ң��ÿ�ѧ��������ʾ�� ����
A. 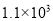 Ԫ B.
Ԫ B. 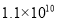 Ԫ C.
Ԫ C. 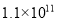 Ԫ D.
Ԫ D. 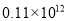 Ԫ
Ԫ
���м�����ȷ���ǣ� ����
A. 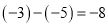 B.
B. 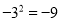 C.
C. 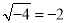 D.
D. 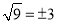
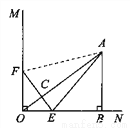
��ͼ����֪��MON=90º��A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=1��ʱ����EOF�릤ABO�Ƿ����ƣ���˵�����ɡ�
��2�����˶������У�����tȡ��ֵʱ������EF��OA��Ϊʲô��
��3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF=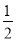 S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�
S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�
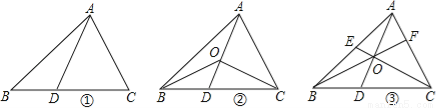
��ͼ���ڡ�ABC�У�D��BC���ϵĵ㣨�����B��C�غϣ�������AD��
�������룺
��1����ͼ�٣�����D��BC���ϵ��е�ʱ��S��ABD��S��ABC=�� ��������D��BC��������һ��ʱ��S��ABD��S��ABC=�� ������ͼ�������߶α�ʾ����
̽���о���
��2����ͼ�ڣ��ڡ�ABC�У�O�����߶�AD��һ�㣨�����A��D�غϣ�������BO��CO���Բ���S��BOC��S��ABC֮��Ӧ�õ���ͼ���������߶�֮�ȣ���˵�����ɣ�
��չӦ�ã�
��3����ͼ�ۣ�O���߶�AD��һ�㣨�����A��D�غϣ�������BO���ӳ���AC�ڵ�F������CO���ӳ���AB�ڵ�E���Բ���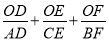 ��ֵ����˵�����ɣ�
��ֵ����˵�����ɣ�
��ͼ�� ����������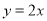 ��ͼ���뷴��������
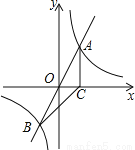
��ͼ���뷴��������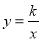 ��ͼ����A��B���㣬����A��AC��ֱx���ڵ�C������BC������ABC���Ϊ 2.
��ͼ����A��B���㣬����A��AC��ֱx���ڵ�C������BC������ABC���Ϊ 2.
��1����k��ֵ
��2��x�����Ƿ����һ��D��ʹ��ABD����ABΪб�ߵ�ֱ�������Σ������ڣ������D�����꣬�������ڣ�˵�����ɡ�
- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������

