题目内容
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线 与y轴交于点C,与抛物线交于点C,D.
与y轴交于点C,与抛物线交于点C,D.
(1)求抛物线的解析式;
(2)求点A到直线CD的距离;
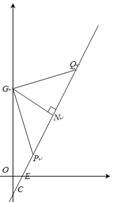
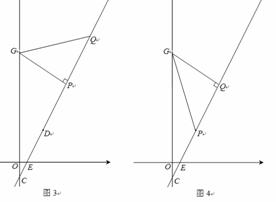
(3)平移抛物线,使抛物线的顶点P在直线CD上,抛物线与直线CD的另一个交点为Q,点G在y轴正半轴上,当以G,P,Q三点为顶点的三角形为等腰直角三角形时,求出所有符合条件的G点的坐标.

(1)
解:在 中,令
中,令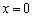 ,得
,得
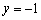 .
.
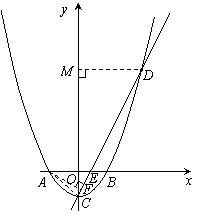 ∴C(0,-1)
∴C(0,-1)
∵抛物线与x轴交于A(-1,0), B(1,0),
∴C为抛物线的顶点.
设抛物线的解析式为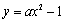 ,
,
将A(-1,0)代入,得 0=a-1.
∴a=1.
∴抛物线的解析式为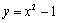 .
.
(2)(本小问5分)
方法一:
 设直线
设直线 与x轴交于E,
与x轴交于E,
则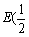 ,0).
,0).
∴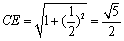 ,
,
 .
.
连接AC,过A作AF⊥CD,垂足为F,
S△CAE 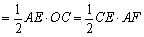 ,
,
即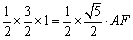 ,
,
∴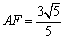 .
.
方法二:由方法一知,
∠AFE=90°,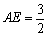 ,
,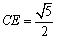 .
.
在△COE与△AFE中,
∠COE=∠AFE=90°,
∠CEO=∠AEF,
∴△COE∽△AFE .
∴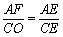 ,
,
即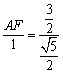 .
.
∴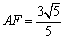 .
.
(3)(本小问5分)
由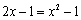 ,得
,得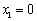 ,
,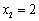 .
.
∴D(2,3).
如图1,过D作y轴的垂线,垂足为M,
由勾股定理,得
 .
.
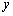 在抛物线的平移过程中,PQ=CD.
在抛物线的平移过程中,PQ=CD.
(i)当PQ为斜边时,设PQ中点为N,G(0,b),
则GN=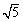 .
.
∵∠GNC=∠EOC=90°,∠GCN=∠ECO,
∴△GNC ∽△EOC.
∴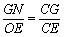 ,
,
∴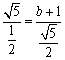 ,
,
∴b=4.
∴G(0,4) .
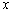 (ii)当P为直角顶点时,
(ii)当P为直角顶点时,
设G(0,b),
则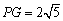 ,
,
同(i)可得b=9,
则G(0,9) .
(iii)当Q为直角顶点时,
同(ii)可得G(0,9) .
综上所述,符合条件的点G有两个,分别是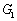 (0,4),
(0,4),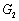 (0,9).
(0,9).

下列命题中:①若a>b,c≠0,则ac>bc;②若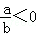 ,则a<0,b>0;③若ac2>bc2,则a>b;④若a<b<0,则
,则a<0,b>0;③若ac2>bc2,则a>b;④若a<b<0,则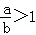 ;⑤若
;⑤若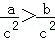 ,则a>b.正确的有( )个.
,则a>b.正确的有( )个.
|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):
A:加强交通法规学习;B:实行牌照管理;C:加大交通违法处罚力度;D:纳入机动车管理;E:分时间分路段限行.
调查数据的部分统计结果如下表:
| 管理措施 | 回答人数 | 百分比 |
| A | 25 | 5% |
| B | 100 | m |
| C | 75 | 15% |
| D | n | 35% |
| E | 125 | 25% |
| 合计 | a | 100% |
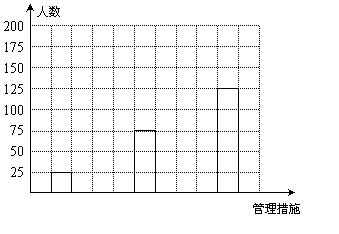
 |
(第21题图)
(1)根据上述统计表中的数据可得m =_______,n =______,a =________;
(2)在答题卡中,补全条形统计图;
(3)该社区有居民2600人,根据上述调查结果,请你估计选择“D:纳入机动车管理”的居民约有多少人?
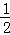 AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点;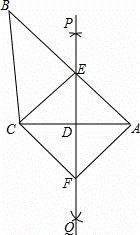
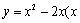 ≥
≥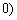 的图象为
的图象为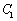 ,
,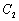 ,则直线
,则直线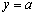 (a为常数)与
(a为常数)与 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
 ( )
( ) 
 ;
;