题目内容
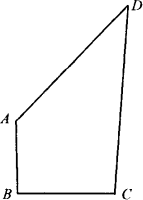
四边形的四条边AB、BC、CD、DA的长分别为3、4、13、12,其中∠B=90°,则四边形的面积是 ( )
A.72 B.66 C.42 D.36
【答案】
D
【解析】
试题分析:先根据题意画出图形,由勾股定理求出AC的值,再根据勾股定理的逆定理判断出△ACD的形状,根据三角形的面积公式求解即可.
如图所示:连接AC,

∵AB=3,BC=4,∠CBA=90°,
∴AC=5,
∵△ACD中,52+122=132,即AC2+AD2=AC2,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ABC+S△ACD= ×3×4+
×3×4+ ×5×12=36.
×5×12=36.
故选D.
考点:本题考查的是勾股定理及勾股定理的逆定理
点评:根据题意画出图形,判断出△ACD的形状是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
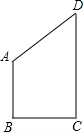 如图,四边形的四条边AB,BC,CD和DA的长分别是2,
如图,四边形的四条边AB,BC,CD和DA的长分别是2,| 5 |
A、
| ||||
B、5
| ||||
C、2(
| ||||
D、
|