题目内容
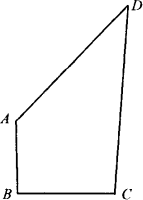
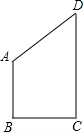 如图,四边形的四条边AB,BC,CD和DA的长分别是2,
如图,四边形的四条边AB,BC,CD和DA的长分别是2,| 5 |
A、
| ||||
B、5
| ||||
C、2(
| ||||
D、
|
分析:首先连接AC,在直角△ABC中,利用勾股定理即可求得AC的长,在△ACD中,利用勾股定理的逆定理即可证得△ACD是直角三角形,根据四边形ABCD的面积=S△ACD+S△ABC即可求解.
解答: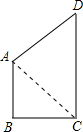 解:连接AC.
解:连接AC.
在直角△ABC中,AC=
=
=3.
∵32+42=52,
∴AC2+AD2=CD2,
∴△ACD是直角三角形,∠DAC=90°.
∴S△ACD=
AC•AD=
×3×4=6,S△ABC=
AB•BC=
×2×
=
,
∴四边形ABCD的面积=S△ACD+S△ABC=
+6.
故选D.
 解:连接AC.
解:连接AC.在直角△ABC中,AC=
| AB2+BC2 |
22+(
|
∵32+42=52,
∴AC2+AD2=CD2,
∴△ACD是直角三角形,∠DAC=90°.
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∴四边形ABCD的面积=S△ACD+S△ABC=
| 5 |
故选D.
点评:本题考查了勾股定理和勾股定理的逆定理,把求不规则的四边形的面积转化为两个直角三角形的面积的和,关键是证明△ACD是直角三角形.

练习册系列答案
相关题目
 5、如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形的四条边为边向外作四个正方形,若S1+S4=100,S3=36,则S2=( )
5、如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形的四条边为边向外作四个正方形,若S1+S4=100,S3=36,则S2=( )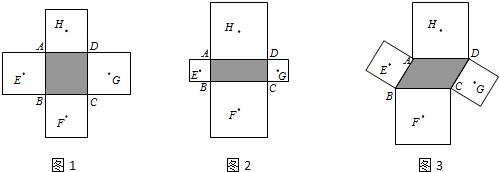
 1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.