题目内容
3.已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.(1)求证:无论k取何值时,方程总有两个不相等的实数根;
(2)若方程的两根x1、x2是斜边长为5的直角三角形两直角边长,求k的值.
分析 (1)先根据判别式的值得到△=1,然后根据判别式的意义可判断方程总有两个不相等的实数根;
(2)根据根与系数的关系得到x1+x2=2k+1,x1x2=k2+k,再根据勾股定理得到x12+x22=52,接着利用完全平方公式变形得到(x1+x2)2-2x1x2=25,则(2k+1)2-2(k2+k)=25,然后解方程后利用方程的两根为正数确定k的值.
解答 (1)证明:△=(2k+1)2-4(k2+k)
=1>0,
所以无论k取何值时,方程总有两个不相等的实数根;
(2)解:x1+x2=2k+1,x1x2=k2+k,
∵x12+x22=52,
∴(x1+x2)2-2x1x2=25,
∴(2k+1)2-2(k2+k)=25,
整理得k2+k-12=0,解得k1=3,k2=-4,
∵x1+x2=2k+1>0,x1x2=k2+k>0,
∴k的值为3.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,反过来也成立.也考查了根的判别式.

练习册系列答案
相关题目
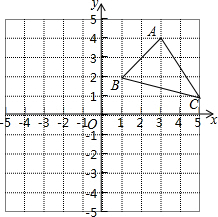 如图,在所给网格图(每小格边长均为1的正方形)中完成下列各题:
如图,在所给网格图(每小格边长均为1的正方形)中完成下列各题: