题目内容
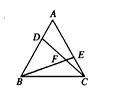
如图所示，以等边三角形ABC的边BC为直径作⊙O交AB于D，交AC于E，判断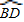
，
，
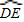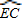之间的大小关系，并说明理由．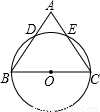
【答案】分析：连接OD，OE，由∠B=∠C=60°，易证△BOD与△COE都是等边三角形，可得∠DOE=∠BOD=∠COE=60°，由圆周角定理知，
．
解答：
解：相等．
如右图所示，连接OD，OE，
∵OB=OD=OE=OC，∠B=∠C=60°
∴△BOD与△COE都是等边三角形
∴∠BOD=∠COE=60°
∠DOE=180°-∠BOD-∠COE=60°
∴∠DOE=∠BOD=∠COE
∴
．
点评：本题利用了等边三角形的性质和判定及圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
．解答：
解：相等．如右图所示，连接OD，OE，
∵OB=OD=OE=OC，∠B=∠C=60°
∴△BOD与△COE都是等边三角形
∴∠BOD=∠COE=60°
∠DOE=180°-∠BOD-∠COE=60°
∴∠DOE=∠BOD=∠COE
∴
．点评：本题利用了等边三角形的性质和判定及圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
如图所示，以等边三角形ABC的边BC为直径作⊙O交AB于D，交AC于E，判断
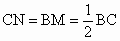，连接MD、NE，则MD、NE与⊙O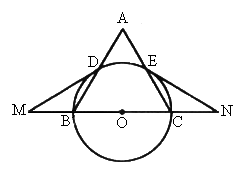
如图所示，以等边三角形ABC的边BC为直径作⊙O交AB于D，交AC于E，判断
，
，
之间的大小关系，并说明理由．