题目内容
13.计算:1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+$\frac{1}{1+2+3+4}$+…+$\frac{1}{1+2+3+…+100}$=$\frac{200}{101}$.分析 利用1+2+3+…+n=$\frac{1}{2}$n(n+1),把分母计算提取2,再进一步拆分求得答案即可.
解答 解:原式=2×($\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{100×101}$)
=2×($\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{100}$-$\frac{1}{101}$)
=2×(1-$\frac{1}{101}$)
=$\frac{200}{101}$.
故答案为:$\frac{200}{101}$.
点评 此题考查有理数的混合运算,找出分母的运算规律,并把分数进行拆分是解决问题的关键.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为4,点P是对角线BD的上一点,PE⊥BC于点E,PF⊥CD于点F,则PA+PE+PF的最小值是4+2$\sqrt{2}$.
如图,正方形ABCD的边长为4,点P是对角线BD的上一点,PE⊥BC于点E,PF⊥CD于点F,则PA+PE+PF的最小值是4+2$\sqrt{2}$.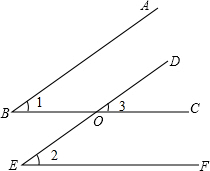 如图所示,有3个论断:①AB∥DE;②∠1=∠2;③BC∥EF.
如图所示,有3个论断:①AB∥DE;②∠1=∠2;③BC∥EF. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象得出下列信息:①甲乙两地相距1200km;②当慢车行驶6h时,慢车和快车相遇;③慢车的速度为80km/h,快车的速度为120km/h;④图中点C的实际意义表示快车刚刚到达乙地时与慢车之间距离.其中正确的信息有( )
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象得出下列信息:①甲乙两地相距1200km;②当慢车行驶6h时,慢车和快车相遇;③慢车的速度为80km/h,快车的速度为120km/h;④图中点C的实际意义表示快车刚刚到达乙地时与慢车之间距离.其中正确的信息有( )