题目内容
O是△ABC的外心,且∠BOC=140°,则∠A=分析:结合题意,可知O为△ABC的外心,即⊙O为△ABC的外接圆,因为∠BOC=140°,利用圆周角定理可知∠BAC=
∠BOC=70°,即可得答案.
再根据三角形的外接圆得到∠ABC=2∠IBC,∠ACB=2∠ICB,根据三角形的内角和定理求出∠IBC+∠ICB,求出∠ACB+∠ABC的度数即可.
| 1 |
| 2 |
再根据三角形的外接圆得到∠ABC=2∠IBC,∠ACB=2∠ICB,根据三角形的内角和定理求出∠IBC+∠ICB,求出∠ACB+∠ABC的度数即可.
解答: 解:根据题意,0为锐角△ABC的外心,∠BOC=140°,
解:根据题意,0为锐角△ABC的外心,∠BOC=140°,
∠BAC=
∠BOC=70°.
∵点I是△ABC的内心,
∴∠ABC=2∠IBC,∠ACB=2∠ICB,
∵∠BIC=140°,
∴∠IBC+∠ICB=180°-∠CIB=40°,
∴∠ABC+∠ACB=2×40°=80°,
∴∠BAC=180°-(∠ACB+∠ABC)=100°.
故答案为:70°,100°.
 解:根据题意,0为锐角△ABC的外心,∠BOC=140°,
解:根据题意,0为锐角△ABC的外心,∠BOC=140°,∠BAC=
| 1 |
| 2 |
∵点I是△ABC的内心,
∴∠ABC=2∠IBC,∠ACB=2∠ICB,
∵∠BIC=140°,
∴∠IBC+∠ICB=180°-∠CIB=40°,
∴∠ABC+∠ACB=2×40°=80°,
∴∠BAC=180°-(∠ACB+∠ABC)=100°.
故答案为:70°,100°.
点评:此题主要考查的是圆周角定理在三角形的外接圆中的应用以及三角形的内心的性质,属于常考类型,正确区分三角形的内外心是解题关键.

练习册系列答案
相关题目
 如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF=( )
如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF=( )| A、a:b:c | ||||||
B、
| ||||||
| C、cosA:cosB:cosC | ||||||
| D、sinA:sinB:sinC |
 )两点,设OA•OB=3(O为坐标系原点).
)两点,设OA•OB=3(O为坐标系原点).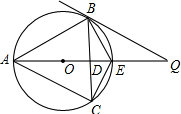 在△ABC中,AB=BC,点O是△ABC的外心,连接AO并延长交BC于D,交△ABC的外接圆于E,过点B作⊙O的切线交AO的延长线于Q,设OQ=
在△ABC中,AB=BC,点O是△ABC的外心,连接AO并延长交BC于D,交△ABC的外接圆于E,过点B作⊙O的切线交AO的延长线于Q,设OQ= 如图,⊙O是△ABC的
如图,⊙O是△ABC的