题目内容
已知点I是△ABC的内心，∠BIC=110°，则∠BAC=分析：（1）I是△ABC的内心，求出角B和角C的和，再利用三角形内角关系，求出∠BAC．
（2）利用圆周角是圆心角的一半即可得出答案．
（2）利用圆周角是圆心角的一半即可得出答案．
解答：解：∵∠B+∠C=2（180°-∠BIC）=140°，
∴∠BAC=180°-140°=40°；
当△ABC是锐角三角形时，∠BAC=
∠BOC=110°×
=55°；
当△ABC是顿角三角形时，∠BAC=180°-55°=125°．
故答案为：40°；55°或125°．
∴∠BAC=180°-140°=40°；
当△ABC是锐角三角形时，∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
当△ABC是顿角三角形时，∠BAC=180°-55°=125°．
故答案为：40°；55°或125°．
点评：考查了三角形内角和以及内心，外心的性质．
练习册系列答案
相关题目
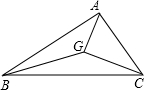如图，已知点G是△ABC的重心，AG=5，GC=12，AC=13，则BG=
18、如图，已知点D是△ABC的边BC（不含点B，C）上的一点，DE∥AB交AC于点E，DF∥AC交AB于点F、要使四边形AFDE是矩形，则在△ABC中要增加的一个条件是：