Question

如图，在△ABC中，∠ABC=90°，∠C=30°，将△ABC绕点A逆时针旋转至△ADE的位置，点B落在边AC上的点D处，连接BE交AC于点F，则tan∠EFD的值为

 

．

Answer 1

考点：相似三角形的判定与性质,解直角三角形

专题：

分析：首先连接BD，由旋转的性质，易证得△ABD是等边三角形，继而可证得AE∥BD，则可证得△AEF∽△DBF，然后由相似三角形的对应边成比例，可求得DF=

1

3

a，继而求得答案．

解答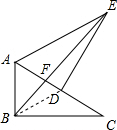： 解：连接BD．
设AB=a，则AD=AB=a，AC=AE=2a，BC=DE=

3

a，
∵在△ABD 中，∠BAD=60°，AB=AD，
∴△ABD是等边三角形．
∴BD=AB=a，∠ADB=60°，
又∵∠EAD=60°，
∴∠EAD=∠ADB，
∴AE∥BD，
∴△AEF∽△DBF，
∴

AE

DB

=

AF

DF

=2，
∴DF=

1

3

AD=

1

3

a，
∴tan∠EFD=

DE

DF

=

3

1 3

=3

3

．
故答案为：3

3

．

点评：此题考查了相似三角形的判定与性质、旋转的性质、等边三角形的判定与性质以及三角函数的定义．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．