题目内容
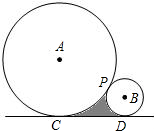 如图,⊙A和⊙B外切于点P,它们的半径分别为0.6m和0.2m,直线CD与它们都相切,切点分别为C、D,求图中阴影部分的面积(精确到0.01m2).
如图,⊙A和⊙B外切于点P,它们的半径分别为0.6m和0.2m,直线CD与它们都相切,切点分别为C、D,求图中阴影部分的面积(精确到0.01m2).(友情提示:通过构造一个直角梯形,求出圆心角的度数)
分析:连接AC、AB、BD,要求阴影部分的面积,即为梯形ABDC的面积减去扇形APC和BPD的面积,即转化为求梯形的面积和两个扇形的面积,AC和BD已知,过点B作BE垂直AC于E,易得BE的长,即梯形的高得知,可得S梯形ACDB;同时可求得∠A和∠B的度数,根据扇形的面积公式,即可分别得出S扇形DBP和S扇形ACP.
解答: 解:连接AB、AC、BD,
解:连接AB、AC、BD,
作BE⊥AC于E.
则四边形CDBE为矩形,
四边形ACDB为梯形,
∴AE=AC-BD=0.4,
AB=AP+BP=0.8
∴在Rt△AEB中,
可得∠ABE=30°,
BE=
∴∠A=60°,∠ABD=120°
∴梯形ACDB的面积
=
(BD+AC)•CD=
(m2)
∴S扇形ACP=
=0.06π(m2)
S扇形DBP=
=
π(m2)
S阴影=S梯形ACDB-S扇形ACP-S扇形DBP=
-0.06π-
π≈0.05(m2).
 解:连接AB、AC、BD,
解:连接AB、AC、BD,作BE⊥AC于E.
则四边形CDBE为矩形,
四边形ACDB为梯形,
∴AE=AC-BD=0.4,
AB=AP+BP=0.8
∴在Rt△AEB中,
可得∠ABE=30°,
BE=
| 2 |
| 5 |
| 3 |
∴∠A=60°,∠ABD=120°
∴梯形ACDB的面积
=
| 1 |
| 2 |
| 4 |
| 25 |
| 3 |
∴S扇形ACP=
| 60×π×0.62 |
| 360 |
S扇形DBP=
| 120×π×0.22 |
| 360 |
| 0.04 |
| 3 |
S阴影=S梯形ACDB-S扇形ACP-S扇形DBP=
| 4 |
| 25 |
| 3 |
| 0.04 |
| 3 |
点评:本题考综合考查了圆与圆的位置关系,梯形和扇形的面积公式和求解直角三角形的知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
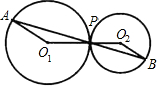 如图,⊙O1和⊙O2外切于点P,过点P的直线AB分别交⊙O1,⊙O2于点A,B.已知⊙O1和⊙O2的面积比是3:1,则AP:BP=( )
如图,⊙O1和⊙O2外切于点P,过点P的直线AB分别交⊙O1,⊙O2于点A,B.已知⊙O1和⊙O2的面积比是3:1,则AP:BP=( )| A、3:1 | ||
| B、6:1 | ||
| C、9:1 | ||
D、
|
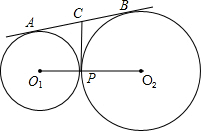 如图,⊙O1和⊙O2外切于点P,内公切线PC与外公切线AB(A、B分别是⊙O1和⊙O2上的切点)相交于点C,已知⊙O1和⊙O2的半径分别为3和4,则PC的长等于
如图,⊙O1和⊙O2外切于点P,内公切线PC与外公切线AB(A、B分别是⊙O1和⊙O2上的切点)相交于点C,已知⊙O1和⊙O2的半径分别为3和4,则PC的长等于 16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC.
16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC.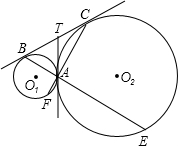 切线,AT与BC相交于点T.延长BA、CA,分别与两圆交于点E、F.
切线,AT与BC相交于点T.延长BA、CA,分别与两圆交于点E、F.