题目内容
如图,∠AOB=60°,P、Q两点分别由O点沿OA、OB方向同时移动,移动速度分别为a米/秒和b米/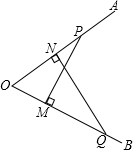 秒,过P、Q分别作PM⊥OB于M,QN⊥OA于N,求:
秒,过P、Q分别作PM⊥OB于M,QN⊥OA于N,求:(1)△POM与△QON的周长之比与面积之比;
(2)若在移动过程中,P与N重合时,求
| a | b |
分析:(1)欲求△POM与△QON的周长之比与面积之比,可以证明△PMO∽△QNO得出;
(2)由于∠AOB=60°,通过三角函数的知识能够求出
的值.
(2)由于∠AOB=60°,通过三角函数的知识能够求出
| a |
| b |
解答:解:(1)设运动了t秒,则OP=at,OQ=bt
∵PM⊥OB,QN⊥OA
∴∠PMO=∠QNO=90°,∠O=∠O
∴△PMO∽△QNO(3分)
∴
=
=
=
∴
=(
)2=(
)2=
(6分)
(2)∵∠AOB=60°
∴OM=
OP=
at(9分)
由(1)得
=
即
=
=
(12分)
∵PM⊥OB,QN⊥OA
∴∠PMO=∠QNO=90°,∠O=∠O
∴△PMO∽△QNO(3分)
∴
| C△POM |
| C△QNO |
| PO |
| QO |
| at |
| bt |
| a |
| b |
∴
| S△POM |
| S△QNO |
| PO |
| QO |
| a |
| b |
| a2 |
| b2 |
(2)∵∠AOB=60°
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
由(1)得
| PO |
| QO |
| OM |
| PO |
即
| a |
| b |
| ||
| a |
| 1 |
| 2 |
点评:本题考查了相似三角形的判定和性质,及三角函数的知识.相似三角形的周长比等于相似比,面积比是相似比的平方.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
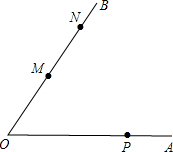 如图,∠AOB=60°,M,N是OB上的点,OM=4,MN=
如图,∠AOB=60°,M,N是OB上的点,OM=4,MN=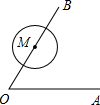 如图,∠AOB=60°,点M是射线OB上的点,OM=4,以点M为圆心,2cm为半径作圆.若OA绕点O按逆时针方向旋转,当OA和⊙M相切时,OA旋转的角度是
如图,∠AOB=60°,点M是射线OB上的点,OM=4,以点M为圆心,2cm为半径作圆.若OA绕点O按逆时针方向旋转,当OA和⊙M相切时,OA旋转的角度是 (2012•金华模拟)如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA,OB上的动点,当△PEF的周长最小时,点P到EF距离是( )
(2012•金华模拟)如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA,OB上的动点,当△PEF的周长最小时,点P到EF距离是( )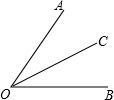 如图,∠AOB=60°,OC是∠AOB的平分线,则∠AOC=
如图,∠AOB=60°,OC是∠AOB的平分线,则∠AOC=