Question

（2012•金华模拟）如图，∠AOB=60°，点P在∠AOB的角平分线上，OP=10cm，点E、F是∠AOB两边OA，OB上的动点，当△PEF的周长最小时，点P到EF距离是（　　）

• A．10cm
• B．5cm
• C．5

  5

• D．5

  3

Answer 1

分析：作P关于OA的对称点，以及关于OB的对称点，连接两个对称点，交OA、OB分别于E、F，则此时△PEF的周长最小，则PM的长度就是所求的量，利用直角三角形的性质即可求解．

解答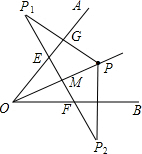：解：作P关于OA的对称点，以及关于OB的对称点，连接两个对称点，交OA、OB分别于E、F，则此时△PEF的周长最小，
∵点P在∠AOB的角平分线上，
∴∠AOP=

1

2

∠AOB=30°，
∴直角△OPG中，PG=

1

2

OP=5cm．
∴PP₁=2PG=10cm．
∵∠P₁PP₂=360°-90°-90°-60°=120°，
∴∠P1PO=60°，
∴∠P₁=30°，
∴PM=

1

2

PP₁=5cm．
故选B．

点评：本题考查了直角三角形的性质：直角三角形中30度的锐角所对的直角边等于斜边的一半，以及最短路径问题，正确确定E、F的位置是关键．