题目内容
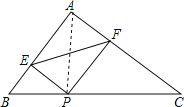
【题目】如图，在Rt△ABC中，∠A=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，则EF的最小值为（ ）
A.2B.2.2C.2.4D.2.5
【答案】C
【解析】
根据已知得出四边形AEPF是矩形，得出EF=AP，要使EF最小，只要AP最小即可，根据垂线段最短得出即可．
解：连接AP，
∵∠A=90°，PE⊥AB，PF⊥AC，
∴∠A=∠AEP=∠AFP=90°，
∴四边形AFPE是矩形，
∴EF=AP，
要使EF最小，只要AP最小即可，
过A作AP⊥BC于P，此时AP最小，
在Rt△BAC中，∠A=90°，AC=4，AB=3，由勾股定理得：BC=5，
由三角形面积公式得：
，
∴AP=2.4，
即EF=2.4，
故选：C．
全优点练单元计划系列答案
【题目】学完二次根式一章后，小易同学看到这样一题：“函数
中,自变量
的取值范围是什么？”这个问题很简单，根据二次根式的性质很容易得到自变量的取值范围.联想到一次函数，小易想进一步研究这个函数的图象和性质.以下是他的研究步骤：
第一步：函数中,自变量的取值范围是_____________.
第二步：根据自变量取值范围列表：
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
__________.
第三步：描点画出函数图象.
在描点的时候，遇到了
，
这样的点，小易同学用所学勾股定理的知识，找到了画图方法，如图所示：
你能否从中得到启发，在下面的
轴上标出表示
、
、
的点，并画出的函数图象.
第四步：分析函数的性质.
请写出你发现的函数的性质(至少写两条)：
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步：利用函数图象解含二次根式的方程和不等式.
（1）请在上面坐标系中画出
的图象，并估算方程
的解.
（2）不等式
的解是__________________.
