Question

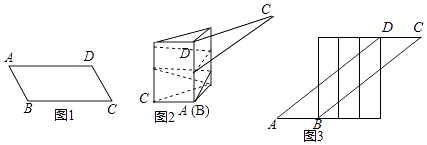
【题目】如图①，OP为一墙面，它与地面OQ垂直，有一根木棒AB如图放置，点C是它的中点，现在将木棒的A点在OP上由A点向下滑动，点B由O点向OQ方向滑动，直到AB横放在地面为止．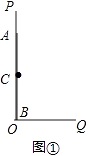

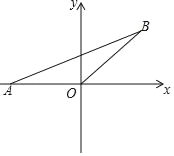
（1）在AB滑动过程中，点C经过的路径可以用下列哪个图象来描述（ ）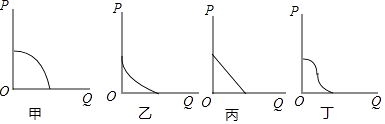

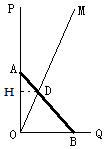
（2）若木棒长度为2m，如图②射线OM与地面夹角∠MOQ=60°，当AB滑动过程中，与OM并于点D，分别求出当AD= 、AD=1、AD= 时，OD的值．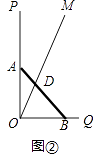

（3）如图③，是一个城市下水道，下水道入口宽40cm，下水道水平段高度为40cm，现在要想把整根木棒AB通入下水道水平段进行工作，那么这根木棒最长可以是（cm）（直接写出结果，结果四舍五入取整数）．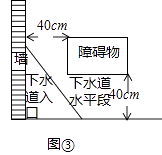

Answer 1

【答案】
（1）甲

（2）解：过D作DH⊥OP于H，设DH=a，在Rt△OHD中，

∵∠AOD=90°﹣600=300，

∴OD=2a，OH= a，

∵DH⊥OA，OQ⊥OA，

∴DH∥QO，

∴ = ，

当AD= 时，BD= ，

∴ = ，

∴AH= a，

在Rt△AHD中，

∵AH2+DH2=AD2，

∴ a2+a2= ，

解得a= ，OD= ，

当AD=1时，BD=1，

∴ = ，

∴AH= a，

在Rt△AHD中，∵AH2+DH2=AD2，

∴3a2+a2=1，

解得a= ，OD=1，

当AD= 时，BD= ，

∴ = ，

∴AH=2 a，

在Rt△AHD中，∵AH2+DH2=AD2，

∴12a2+a2= ，

解得a= ，OD=

（3）113
【解析】解：（1）∵点C是AB的中点，

∴OC= AB，

∴点C的运动轨迹是以O为圆心， AB长为半径的圆弧，经过的路程的 圆周．

故选甲．（3）由题意当等腰直角三角形的直角边为80cm时，斜边为 ≈113cm，

所以这根木棒最长可以是113cm．

所以答案是113cm．

【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识，掌握对应角相等，对应边成比例的两个三角形叫做相似三角形．