Question

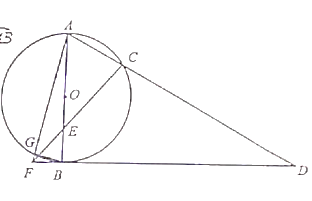
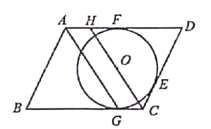
【题目】如图，平行四边形分别切于点，连接并延长交于点，连接与刚好平行，若，则的直径为______．

Answer 1

【答案】

【解析】

先证得四边形AGCH是平行四边形，则，再证得，求得 ，证得DO⊥HC，根据，即可求得半径，从而求得结论．

∵四边形ABCD是平行四边形，

∴AD∥BC，

∵AG∥HC，

∴四边形AGCH是平行四边形，

∴，

∵是⊙O的切线，且切点为、，

∴，∠GCH=∠HCD，

∵AD∥BC，

∴∠DHC=∠GCH，

∴∠DHC=∠HCD，

∴三角形DHC为等腰三角形，

∴，

∴，

∴，，

连接OD、OE，如图，

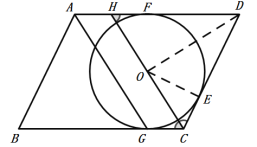
∵是⊙O的切线，且切点为、，

∴DO是∠FDE的平分线，

又∵，

∴DO⊥HC,

∴∠DOC=90，

∵切⊙O于，

∴OE⊥CD,

∵∠OCE+∠COE=90，∠DOE+∠COE=90，

∴∠OCE=∠DOE，

∴，

∴，即，

∴，

∴⊙O的直径为：

故答案为：．