��Ŀ����
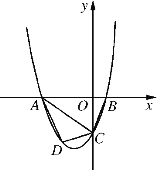
����Ŀ����ͼ�����κ���y=a��x2��4mx��12m2��������a��m�dz�������a��0��m��0����ͼ����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ��C��0����6������D�ڶ��κ�����ͼ���ϣ�CD��AB������AD������A������AE�����κ�����ͼ���ڵ�E��ABƽ�֡�DAE��
��1���ú�m�Ĵ���ʽ��ʾa��
��2����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
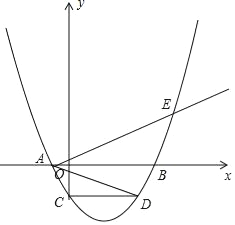
��3����ö��κ���ͼ��Ķ���ΪF������FC���ӳ���x��ĸ������ڵ�G���ж����߶�GF��AD��AE�ij���Ϊ���߳��������ε�����Ƿ���Ϊ24��![]() +1��m2��48
+1��m2��48![]() m��72
m��72![]() +24���������m��������˵�����ɣ�
+24���������m��������˵�����ɣ�
���𰸡���1��a=![]() ����2������������3��m=3��
����2������������3��m=3��
��������
��1���ѵ�C�������y=a��x2��4mx��12m2���У����ɽ�����⣮
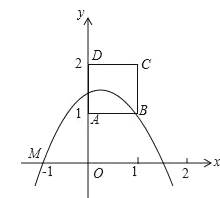
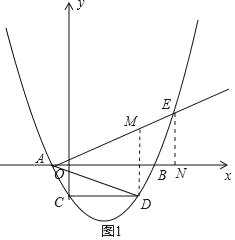
��2����ͼ1������D��E�ֱ���x��Ĵ��ߣ�����ΪM��N���������A��B�������꣬�ɡ�ADM�ס�AEN���Ƴ�![]() ��E����Ϊ
��E����Ϊ![]() �ɵ�
�ɵ�![]() �Ƴ�x=8m���ɵ�E��8m��10������AM=AO+OM=2m+4m=6m��AN=AO+ON=2m+8m=10m���ɴ˼��ɽ�����⣮
�Ƴ�x=8m���ɵ�E��8m��10������AM=AO+OM=2m+4m=6m��AN=AO+ON=2m+8m=10m���ɴ˼��ɽ�����⣮
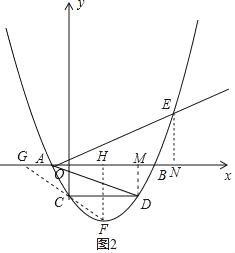
��3����ͼ2���Ƕ��κ���ͼ��ΪF����F������Ϊ��m��-4��������F��FH��x���ڵ�H������FC���ӳ�����x�Ḻ���ύ��һ�㣬�˵㼴Ϊ����ĵ�G��
��![]() �Ƴ�
�Ƴ�![]() ��
��![]() �õ�OG=6m��
�õ�OG=6m��![]() �ɵ�
�ɵ�
AD��GF��AE=3��4��5���ɴ˼��ɽ�����⣮
��1����C��0����6����������y=a��x2��4mx��12m2����
��6=a��0��0��12m2����
���a=![]() ��
��
��2��֤������ͼ1������D��E�ֱ���x��Ĵ��ߣ�����ΪM��N��
��a��x2��4mx��12m2��=0��
���x1=��2m��x2=6m��
���A����2m��0����B��6m��0����
��CD��AB��
���D��������4m����6����
��ABƽ�֡�DAE��
���DAM=��EAN��
���DMA=��ENA=90�㣬
���ADM�ס�AEN��
��![]()
���E����Ϊ![]()
![]()
��x=8m��
��E��8m��10����
��AM=AO+OM=2m+4m=6m��AN=AO+ON=2m+8m=10m��
��![]() ��Ϊ��ֵ��
��Ϊ��ֵ��
��3����ͼ2���Ƕ��κ���ͼ��Ķ���ΪF����F������Ϊ��2m����8��������F��FH��x���ڵ�H��
��![]()
��![]() ��
��![]()
��OG=6m��
��![]()
��![]()
��![]()
��AD��GF��AE=3��4��5��
�����߶�GF��AD��AE�ij���Ϊ���߳�����������ֱ�������Σ�
�����߶�GF��AD��AE�ij���Ϊ���߳��������ε����Ϊ![]()
��![]()
��m=3��m=��1��
��m��0��
��m=3��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�