题目内容
实数x，y满足x≥y≥1和2x2-xy-5x+y+4=0，则x+y= ．
考点：因式分解的应用,非负数的性质：偶次方,配方法的应用
专题：
分析：由原式可以变形为（x-2）2+（x-y）（x-1）=0，根据非负数的性质及条件可以得出，（x-2）2≥0，x≥y≥1，（x-y）（x-1）≥0，从而可以求出x、y的值．
解答：解：∵2x2-xy-5x+y+4=0
∴x2+x2-xy-4x-x+y+4=0
∴x2-4x+4+x（x-y）-（x-y）=0
∴（x-2）2+（x-y）（x-1）=0
∵（x-2）2≥0，x≥y≥1，
∴（x-y）（x-1）≥0
因此两项都非负，只能都为0
∴x=y=2
∴x+y=4．
故答案为：4．
∴x2+x2-xy-4x-x+y+4=0
∴x2-4x+4+x（x-y）-（x-y）=0
∴（x-2）2+（x-y）（x-1）=0
∵（x-2）2≥0，x≥y≥1，
∴（x-y）（x-1）≥0
因此两项都非负，只能都为0
∴x=y=2
∴x+y=4．
故答案为：4．
点评：本题考查了因式分解的运用，非负数的性质，以及配方法的使用．本题具有一定的难度，条件的运用时关键．
练习册系列答案
相关题目
从甲、乙、丙、丁四位同学中任选两人去参加学校合唱队．甲落选的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
方案设计：“春江花月”生活区有一块长36米、宽26米的矩形场地，欲建成一个供居民休闲的小花园．计划在正中央建一个半径为3米的喷水池，其余部分面积的一半进行绿化，现生活区向居民征集设计方案，如果你是小区的居民，请你至少给出两种设计方案（要求美观大方，标出有关数据，并解释其可行性）．
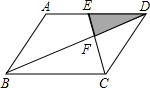如图，?ABCD中，E为AD的中点．已知△DEF的面积为S，则四边形ABFE的面积为（ ）| A、5S | B、6S | C、7S | D、8S |