题目内容
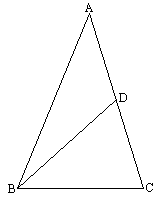
阅读:如图所示,△ABC内接于⊙O,∠CAE=∠B.

求证:AE与⊙O相切于点A.
证明:作直径AF,连结FC,则∠ACF= .
.
∴∠AFC+∠CAF=
∵∠B=∠AFC
∴∠B+∠CAF=
又∵∠CAE=∠B
∴∠CAE+∠CAF= .
.
即AE与⊙O相切于点A.
问题:通过阅读得到的启示证明下题(阅读中的结论可直接应用).
如图所示,已知△ABC内接于⊙O,P是CB延长线上一点,连结AP,且PA2=PB·PC.求证:PA是⊙O的切线.

答案:
解析:
解析:
|
过A作直径AE,证∠PAE= |

练习册系列答案
相关题目

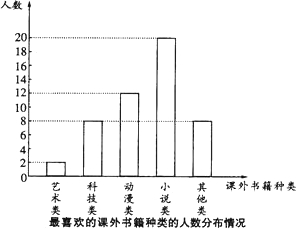 抽取部分同学进行问卷调查,并将调查问卷适当整理后绘制成如图所示的条形统计图.
抽取部分同学进行问卷调查,并将调查问卷适当整理后绘制成如图所示的条形统计图. 20、阅读材料,解答问题.
20、阅读材料,解答问题.