题目内容
已知a,b,c是直角三角形的三条边,且a<b<c,斜边上的高为h,则下列说法中正确的是 ________.(只填序号)
①a2b2+h4=(a2+b2+1)h2;②b4+c2h2=b2c2;③由 可以构成三角形;④直角三角形的面积的最大值是
可以构成三角形;④直角三角形的面积的最大值是 .
.
②
分析:根据直角三角形的面积公式和勾股定理将各式化简,等式成立者即为正确答案.
解答:根据直角三角形的面积的不同算法,
有 ab=
ab= ch,
ch,
解得h= .
.
①将h= 代入a2b2+h4=(a2+b2+1)h2,得
代入a2b2+h4=(a2+b2+1)h2,得
a2b2+( )4=(a2+b2+1)(
)4=(a2+b2+1)( )2,得
)2,得
a2b2+( )4=(c2+1)(
)4=(c2+1)( )2,得
)2,得
a2b2+( )4=a2b2+
)4=a2b2+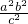 ,得
,得
即( )4=
)4=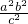 ,
,
a2b2=c2,不一定成立,故本选项错误;
②将h= 代入b4+c2h2=b2c2,得
代入b4+c2h2=b2c2,得
b4+c2( )2=b2c2,
)2=b2c2,
b4+b2a2=b2c2,
整理得b4+b2a2-b2c2=0,
b2(b2+a2-c2)=0,
∵b2+a2-c2=0,
∴b2(b2+a2-c2)=0成立,故本选项正确;
③∵b2+a2=c2,
( )2+(
)2+( )2=a+b,
)2=a+b,
( )2=c,
)2=c,
∴不能说明( )2+(
)2+( )2=(
)2=( )2,
)2,
故本选项错误;
④直角三角形的面积为 ab,随ab的变化而变化,所以无最大值,故本选项错误.
ab,随ab的变化而变化,所以无最大值,故本选项错误.
故答案为②.
点评:此题不仅考查了勾股定理,还考查了面积法求直角三角形的高,等式变形计算较复杂,要仔细.
分析:根据直角三角形的面积公式和勾股定理将各式化简,等式成立者即为正确答案.
解答:根据直角三角形的面积的不同算法,
有
 ab=
ab= ch,
ch,解得h=
 .
.①将h=
 代入a2b2+h4=(a2+b2+1)h2,得
代入a2b2+h4=(a2+b2+1)h2,得a2b2+(
 )4=(a2+b2+1)(
)4=(a2+b2+1)( )2,得
)2,得a2b2+(
 )4=(c2+1)(
)4=(c2+1)( )2,得
)2,得a2b2+(
 )4=a2b2+
)4=a2b2+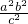 ,得
,得即(
 )4=
)4=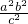 ,
,a2b2=c2,不一定成立,故本选项错误;
②将h=
 代入b4+c2h2=b2c2,得
代入b4+c2h2=b2c2,得b4+c2(
 )2=b2c2,
)2=b2c2,b4+b2a2=b2c2,
整理得b4+b2a2-b2c2=0,
b2(b2+a2-c2)=0,
∵b2+a2-c2=0,
∴b2(b2+a2-c2)=0成立,故本选项正确;
③∵b2+a2=c2,
(
 )2+(
)2+( )2=a+b,
)2=a+b,(
 )2=c,
)2=c,∴不能说明(
 )2+(
)2+( )2=(
)2=( )2,
)2,故本选项错误;
④直角三角形的面积为
 ab,随ab的变化而变化,所以无最大值,故本选项错误.
ab,随ab的变化而变化,所以无最大值,故本选项错误.故答案为②.
点评:此题不仅考查了勾股定理,还考查了面积法求直角三角形的高,等式变形计算较复杂,要仔细.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
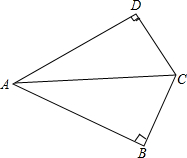 已知:如图,四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.
已知:如图,四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.