题目内容
7.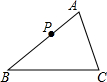 已知△ABC的边AB=6,AC=4,如图所示,取AB的中点P,在AC上再取一点Q,使△APQ与△ABC相似,则AQ的长为2或$\frac{9}{2}$.
已知△ABC的边AB=6,AC=4,如图所示,取AB的中点P,在AC上再取一点Q,使△APQ与△ABC相似,则AQ的长为2或$\frac{9}{2}$.
分析 由△ABC的边AB=6,AC=4,取AB的中点P,可求得AP的长,然后分别从△APQ∽△ABC或△AQP∽△ABC去分析求解即可求得答案.
解答 解:∵△ABC的边AB=6,AC=4,AB的中点P,
∴AP=3,
若△APQ∽△ABC,则AP:AB=AQ:AC,
∴3:6=AQ:4,
解得:AQ=2;
若△AQP∽△ABC,则AP:AC=AQ:AB,
∴3:4=AQ:6,
解得:AQ=$\frac{9}{2}$,
∴AQ的长为2或$\frac{9}{2}$.
故答案为:2或$\frac{9}{2}$.
点评 此题考查了相似三角形的判定.注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.个体儿童服装店老板以32元的价格购进30件连衣裙,针对不同的顾客,30件连衣裙的售价不完全相同,若以47元为标准价,将超过的钱数记为正,不足的钱数记为负,则记录结果如表:
请问:(1)该服装店售完这30件连衣裙的总销售额是多少?
(2)该服装店售完这30件连衣裙赚了多少钱?
| 售出数量/件 | 7 | 6 | 3 | 5 | 4 | 5 |
| 售价/元 | +3 | +2 | +1 | 0 | -1 | -2 |
(2)该服装店售完这30件连衣裙赚了多少钱?
15.若m,n都是正整数,且1≤n<m则下列按字母x的降幂排列是( )
| A. | xm+yn-2xy | B. | yn+xm-2xy | C. | xm-2xy+yn | D. | yn-2xy+xm |
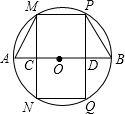 如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q,
如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q, 如图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.
如图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.