题目内容
【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题：
（1）已知，如图1，△ABC中，P点是∠ABC和∠ACB的角平分线的交点，求证：∠P=
∠A+90°。
（2）如图2，若P点是∠ABC和∠ACB外角的角平分线的交点，∠A=80°，那么∠P=____°；
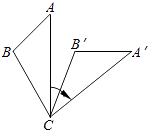
（3）如图3，△ABC中，若P点是∠ABC外角和∠ACB外角的角平分线的交点，∠A=
，那么∠P=________（请用含的代数式表示）
【答案】（1）见解析（2）40°（3）90°-
【解析】
根据角平分线的定义和三角形的外角等于不相邻的两个内角之和，推理出两角的关系。
(1)证明：由三角形内角和定理得，
，
∵点P是
和
的角平分线的交点
∴
∴
又∵
∴
∴
∴
(2)由三角形的外角性质得
∵点P是和外角的角平分线的交点
∴
∴
∴
∵
是
的外角
∴
∴
∴
(3)由三角形内角和定理得
∵点
是外角和外角的角平分线的交点
∴
∴
=
∴
∵
∴
∵
∴
练习册系列答案
相关题目
