题目内容
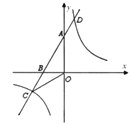
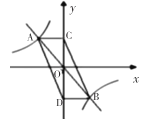
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,过
两点,过![]() 、
、![]() 两点分别作
两点分别作![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )
A.4B.8C.12D.24
【答案】C
【解析】
根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=![]() |k|,得出S△AOC=S△ODB=3,再根据反比例函数的对称性可知:OC=OD,AC=BD,即可求出四边形ACBD的面积.
|k|,得出S△AOC=S△ODB=3,再根据反比例函数的对称性可知:OC=OD,AC=BD,即可求出四边形ACBD的面积.
解:∵过函数![]() 的图象上A,B两点分别作y轴的垂线,垂足分别为点C,D,
的图象上A,B两点分别作y轴的垂线,垂足分别为点C,D,
∴S△AOC=S△ODB=![]() |k|=3,
|k|=3,
又∵OC=OD,AC=BD,
∴S△AOC=S△ODA=S△ODB=S△OBC=3,
∴四边形ABCD的面积为=S△AOC+S△ODA+S△ODB+S△OBC=4×3=12.
故选C.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目