题目内容
3.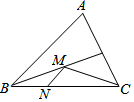 如图,在锐角三角形ABC中,BC=2,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值为$\sqrt{2}$.
如图,在锐角三角形ABC中,BC=2,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值为$\sqrt{2}$.
分析 过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,则CE即为CM+MN的最小值,再根据BC=4,∠ABC=45°,由锐角三角函数的定义即可求出CE的长.
解答  解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,
解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,
∵BD平分∠ABC,
∴M′E=M′N′,
∴M′N′+CM′=EM′+CM′=CE,则CE即为CM+MN的最小值,
∵BC=2,∠ABC=45°,
∴CE=BC•sin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
∴CM+MN的最小值是$\sqrt{2}$.
故答案是:$\sqrt{2}$.
点评 本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
1.下列事件是随机事件的是( )
| A. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 有一名运动员奔跑的速度是30米/秒 | |
| D. | 购买一张福利彩票,中奖 |
18.下列说法中,正确的是( )
| A. | 1的平方根是1 | B. | -1是1的平方根 | C. | 8的立方根是±2 | D. | $\sqrt{9}$=±3 |
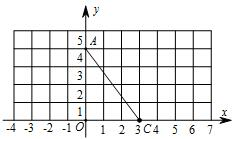 如图,在平面直角坐标系中,A(0,4),C(3,0),
如图,在平面直角坐标系中,A(0,4),C(3,0), 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.
如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.