题目内容
如图，是y=x2、y=x、y=
在同一直角坐标系中图象，请根据图象写出＜x＜x2时x的取值范围是________．
-1＜x＜0或x＞1
分析：先确定出三个函数在第一象限内的交点坐标，y=x与y=在第三象限内交点坐标，然后根据函数图象，找出抛物线图象在最上方，反比例函数图象在最下方的x的取值范围即可．
解答：易求三个函数在第一象限内交点坐标为（1，1），
y=x与y=在第三象限内交点坐标为（-1，-1），
所以，＜x＜x2时x的取值范围是：-1＜x＜0或x＞1．
故答案为：-1＜x＜0或x＞1．
点评：本题考查了二次函数与不等式的关系，数形结合是此类题目求解的重要方法．
分析：先确定出三个函数在第一象限内的交点坐标，y=x与y=
在第三象限内交点坐标，然后根据函数图象，找出抛物线图象在最上方，反比例函数图象在最下方的x的取值范围即可．解答：易求三个函数在第一象限内交点坐标为（1，1），
y=x与y=
在第三象限内交点坐标为（-1，-1），所以，
＜x＜x2时x的取值范围是：-1＜x＜0或x＞1．故答案为：-1＜x＜0或x＞1．
点评：本题考查了二次函数与不等式的关系，数形结合是此类题目求解的重要方法．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
如图，抛物线y=x2+1与双曲线y=| k |
| x |
| k |
| x |
| A、x＞1 | B、x＜-1 |
| C、0＜x＜1 | D、-1＜x＜0 |
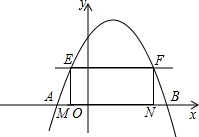行于x轴的直线EF与抛物线交于E，F两点，E在F的左侧，过E，F分别作x轴的垂线，垂足是M，N．
（2013•德宏州）如图，是反比例函数y=
如图，是y=x2、y=x、y=