Question

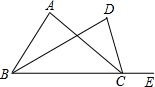已知：如图，∠ABD=∠DBC，∠ACD=∠DCE．
（1）若∠A=50°，求∠D的度数；
（2）猜想∠D与∠A的关系，并说明理由；
（3）若CD∥AB，判断∠ABC与∠A的关系．

Answer 1

分析：关键是运用题目中已知条件的各个角之间的关系进行代换，从而求解．

解答：解：（1）对于△BCD，∠DCE=∠DBC+∠D，
又∵∠ABD=∠DBC，∠ACD=∠DCE，
∴∠ACD=∠ABD+∠D．
又由三角形的外角性质得，∠A+∠ABD=∠D+∠ACD，
由上两式可解得，∠D=

1

2

∠A=25°；

（2）由（1）可得，∠D=

1

2

∠A；

（3）若CD∥AB，则∠ABC=∠DCE，
又∵∠DBC+∠D=∠DCE，
又∵∠D=

1

2

∠A，
则

1

2

∠ABC+

1

2

∠A=∠DCE，
∴∠A=2∠DCE-∠ABC=∠ABC．

点评：灵活运用三角形的外角性质进行求解．