题目内容
17.期末复习二元一次方程组解法时,面对老师给出的方程组:$\left\{\begin{array}{l}{2x+3y=2,…①}\\{2x-6y=-1,…②}\end{array}\right.$,“自由飞翔”小组经过讨论并展示了3种不同的转化方法:(1)①-②,则可得关于y的一元一次方程:9y=3;
(2)①×2+②,则可得关于x的一元一次方程:6x=3;
(3)①+②×2,消去常数项,则可得6x-9y=0,再代入①或②.
分析 (1)两方程相减得到关于y的方程即可;
(2)利用加减消元法消去y得到关于x的方程即可;
(3)利用加减消元法消去常数项即可.
解答 解:(1)①-②,则可得关于y的一元一次方程:9y=3;
(2)①×2+②,则可得关于x的一元一次方程:6x=3;
(3)①+②×2,消去常数项,则可得6x-9y=0,再代入①或②.
故答案为:(1)9y=3;(2)6x=3;(3)6x-9y=0
点评 此题考查了解二元一次方程组,以及解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.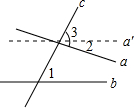 如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( )
如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( )
 如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( )
如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( )| A. | 8° | B. | 10° | C. | 18° | D. | 28° |
2.已知一组数据:2,3,3,5,7,下列说法不正确的是( )
| A. | 平均数是4 | B. | 中位数是5 | C. | 众数是3 | D. | 方差是3.2 |
9. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
6.直线y=2x-3与y=-x+3的交点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.下列运算正确的是( )
| A. | (a3)2=a5 | B. | a2•a3=a5 | C. | a6÷a2=a3 | D. | 3a2-2a2=1 |