题目内容
解方程:
(1)2x2-7x+3=0;
(2)3x(x-1)=2(x-1);
(3)(2x-5)2-(x+4)2=0.
(1)2x2-7x+3=0;
(2)3x(x-1)=2(x-1);
(3)(2x-5)2-(x+4)2=0.
考点:解一元二次方程-因式分解法
专题:
分析:(1)利用因式分解法将方程变形为(2x-1)(x-3)=0,得到2x-1=0或x-3=0,求出x的值即可;
(2)先移项,使方程的右边化为零,再利用因式分解法将方程变形为(x-1)(3x-2)=0,得到x-1=0或3x-2=0,求出x的值即可;
(3)利用因式分解法将方程变形为(2x-5+x+4)(2x-5-x-4)=0,得到3x-1=0或x-9=0,求出x的值即可.
(2)先移项,使方程的右边化为零,再利用因式分解法将方程变形为(x-1)(3x-2)=0,得到x-1=0或3x-2=0,求出x的值即可;
(3)利用因式分解法将方程变形为(2x-5+x+4)(2x-5-x-4)=0,得到3x-1=0或x-9=0,求出x的值即可.
解答:解:(1)∵2x2-7x+3=0,
∴(2x-1)(x-3)=0,
∴2x-1=0或x-3=0,
解得x1=
,x2=3;
(2)3x(x-1)-2(x-1)=0,
(x-1)(3x-2)=0,
x-1=0或3x-2=0,
解得x1=1,x2=
;
(3)(2x-5)2-(x+4)2=0,
(2x-5+x+4)(2x-5-x-4)=0,
3x-1=0或x-9=0,
解得x1=
,x2=9.
∴(2x-1)(x-3)=0,
∴2x-1=0或x-3=0,
解得x1=
| 1 |
| 2 |
(2)3x(x-1)-2(x-1)=0,
(x-1)(3x-2)=0,
x-1=0或3x-2=0,
解得x1=1,x2=
| 2 |
| 3 |
(3)(2x-5)2-(x+4)2=0,
(2x-5+x+4)(2x-5-x-4)=0,
3x-1=0或x-9=0,
解得x1=
| 1 |
| 3 |
点评:本题主要考查了解一元二次方程-因式分解法的知识点,解答本题的关键是把方程的一边能够分解成两个一次因式,此题难度一般.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,∠ABC=60°,BD是△ABC的角平分线,DE⊥AB,垂足为E,若DE=5.求AC的长.
如图,在△ABC中,∠C=90°,∠ABC=60°,BD是△ABC的角平分线,DE⊥AB,垂足为E,若DE=5.求AC的长.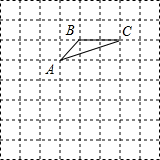 在方格纸上任意连接不在同一直线上的三个格点,便可画出一个三角形.请用这种方式在如下的方格纸上画出两个大小不等的三角形,要求这两个三角形都与格点三角形△ABC相似,且相似比不为1.
在方格纸上任意连接不在同一直线上的三个格点,便可画出一个三角形.请用这种方式在如下的方格纸上画出两个大小不等的三角形,要求这两个三角形都与格点三角形△ABC相似,且相似比不为1.