题目内容
 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,∠BOA=120°,OA=6.
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,∠BOA=120°,OA=6.(1)求弦AB的长;
(2)求图中阴影部分的面积.
考点:切线的性质,垂径定理,扇形面积的计算
专题:
分析:(1)连接OP,利用切线的性质和特殊角的锐角三角函数值即可求出AB的长;
(2)由题意可知阴影部分的面积=等腰三角形AOB的面积-扇形的面积.
(2)由题意可知阴影部分的面积=等腰三角形AOB的面积-扇形的面积.
解答: 解:(1)连接OP,
解:(1)连接OP,
∵大圆的弦AB切小圆于P,
∴OP⊥AB,
∵∠BOA=120°,OA=6.
∴OP=3;
(2)∵OP=3,AO=6
∴AP=3
,
∴AB=6
,
∴等腰三角形AOB的面=
×AB•OP=9
,
∴阴影部分的面积=等腰三角形AOB的面积-扇形的面积=9
-
=9
-3π.
 解:(1)连接OP,
解:(1)连接OP,∵大圆的弦AB切小圆于P,
∴OP⊥AB,
∵∠BOA=120°,OA=6.
∴OP=3;
(2)∵OP=3,AO=6
∴AP=3
| 3 |
∴AB=6
| 3 |
∴等腰三角形AOB的面=
| 1 |
| 2 |
| 3 |
∴阴影部分的面积=等腰三角形AOB的面积-扇形的面积=9
| 3 |
| 120×9π |
| 360 |
| 3 |
点评:本题考查了切线的性质,垂径定理以及勾股定理和扇形面积的计算,是基础知识要熟练掌握.

练习册系列答案
相关题目
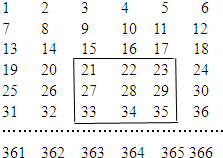 将连续自然数1至366按如图所示的方式排成一个长方形阵列,用一个小正方形任意圈出其中的9个数,设圈出的9个数的中心数为a.
将连续自然数1至366按如图所示的方式排成一个长方形阵列,用一个小正方形任意圈出其中的9个数,设圈出的9个数的中心数为a. 如图,已知∠ACB=90°,BD=BC,AE=AC,则∠DCE=
如图,已知∠ACB=90°,BD=BC,AE=AC,则∠DCE=