题目内容
19.把正确的序号填在横线上①.①菱形四边中点围成的四边形是矩形.
②梯形中位线为a,高为n,则面积为$\frac{1}{2}$ah.
③$\sqrt{{a^2}+{b^2}}$=a+b.
分析 根据中点四边形的判定方法和菱形的性质对①进行判断;根据梯形中位线性质和梯形的面积公式对②进行判断;根据最简二次根式的定义对③进行判断.
解答 解:菱形的对角线互相垂直,则菱形四边中点围成的四边形是矩形,所以①正确;
梯形中位线为a,高为n,则梯形的面积=ah,所以②错误;
$\sqrt{{a^2}+{b^2}}$是最简二次根式,所以③错误.
故答案为①.
点评 本题考查了中点四边形:连结四边形各边中点所得四边形为平行四边形.也考查了二次根式的性质与化简、梯形的中位线性质.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7.下列各式中,不能用平方差公式计算的是( )
| A. | (-x-y)(x-y) | B. | (x-y)(-x+y) | C. | (x+y)(-x+y) | D. | (-x+y)(-x-y) |
14.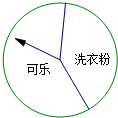 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
(1)完成上述表格;(结果全部精确到0.1)
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“可乐”的概率约是0.6;(结果全部精确到0.1)
(3)转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少度?
 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 604 | |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“可乐”的概率约是0.6;(结果全部精确到0.1)
(3)转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少度?
4.将一个有40个数据的样本统计分成6组,若某一组的频率为0.15,则该组的频数约是( )
| A. | 1 | B. | 0.9 | C. | 6.67 | D. | 6 |
8.下列作图语句正确的是( )
| A. | 作线段AB,使α=AB | B. | 延长线段AB到C,使AC=BC | ||
| C. | 作∠AOB,使∠AOB=∠α | D. | 以O为圆心作弧 |
 如图,在平面直角坐标系中,四边形OABC是菱形,若点A坐标为(4,3),则菱形ABCD的面积是24,周长是20.
如图,在平面直角坐标系中,四边形OABC是菱形,若点A坐标为(4,3),则菱形ABCD的面积是24,周长是20.