题目内容
20.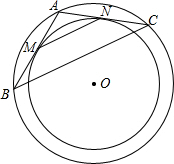 如图,两个同心圆O,大圆的弦AB、AC切小圆于点M、N,连接BC、MN,求证,MN=$\frac{1}{2}$BC.
如图,两个同心圆O,大圆的弦AB、AC切小圆于点M、N,连接BC、MN,求证,MN=$\frac{1}{2}$BC.
分析 连接OM,ON,根据切线的性质得到OM⊥AB,ON⊥AC,由垂径定理得到AM=BM,AN=CN,然后根据三角形的中位线的性质即可得到结论.
解答  解:连接OM,ON,
解:连接OM,ON,
∵AB、AC切小圆于点M、N,
∴OM⊥AB,ON⊥AC,
∴AM=BM,AN=CN,
∴MN=$\frac{1}{2}$BC.
点评 本题主要考查切线的性质,垂径定理,三角形的中位线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.甲、乙两个仓阵要向A、B两地调运小麦.甲可以调出80吨.乙可以调出40吨.A地需要小麦50吨,B需要70吨.
运费如表一:(单位:千米)
运费如表二:(单位:元/吨 千米)
(1)设甲库运往A地x(20≤x≤40)吨求总运费(甲、乙两个仓库的运费之和)y与x之间的函数关系式;
(2)根据(1)中的函数的增减性以及x的取值范围,请确定运费最少的运送方案.
运费如表一:(单位:千米)
| A | B | |
| 甲 | 50 | 40 |
| 乙 | 80 | 25 |
| A | B | |
| 甲 | 2 | 1 |
| 乙 | 1.5 | 2 |
(2)根据(1)中的函数的增减性以及x的取值范围,请确定运费最少的运送方案.
 对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.
对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.
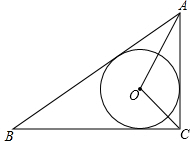 如图所示,⊙O内切于△ABC,若∠ACB=90°,∠AOC=105°,AB=$\frac{8}{3}$,求AC及S△ABC.
如图所示,⊙O内切于△ABC,若∠ACB=90°,∠AOC=105°,AB=$\frac{8}{3}$,求AC及S△ABC.