题目内容
10.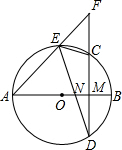 如图,AB为⊙O直径,CD为弦,弦CD⊥AB于点M,F为DC延长线上一点,连接CE、AD、AF,AF交⊙O于E,连接ED交AB于N.
如图,AB为⊙O直径,CD为弦,弦CD⊥AB于点M,F为DC延长线上一点,连接CE、AD、AF,AF交⊙O于E,连接ED交AB于N.(1)求证:∠AED=∠CEF;
(2)当∠F=45°,且BM=MN时,求证:AD=ED;
(3)在(2)的条件下,若MN=1,求FC的长.
分析 (1)首先连接BE,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠AEB=∠BEF=90°,又由AB⊥CD于,可得:$\widehat{BC}=\widehat{BD}$,继而证得∠CMB=∠BMD,则可证得结论;
(2)连接AD,BD,根据已知条件得到∠ADE=∠ABE=∠EAB=45°,证得CD垂直平分BN,得到BD=ND,由等腰三角形的性质得到∠DBN=∠DNB,推出△AEN∽△ADE,根据相似三角形的性质得到∠ANE=∠DAE,等量代换得到∠DAE=∠AED,于是得到结论;
(3)设AB=2R,根据等腰直角三角形的性质得到AE=BE=$\sqrt{2}$R,求得AN=AE=$\sqrt{2}$R,得到R=2+$\sqrt{2}$,解得BE=2$\sqrt{2}$+2,等量代换即可得到结论.
解答 证明:(1)连结BE,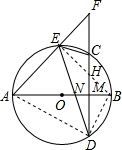 ∵AB是⊙O的直径,
∵AB是⊙O的直径,
∴∠AEB=∠BEF=90°,
又∵AB⊥CD于M,
∴$\widehat{BC}=\widehat{BD}$,
∴∠CEB=∠BED,
∴∠AED=∠AEB-∠BED=∠BEF-∠CEB=∠CEF,
即:∠AED=∠FEC;
(2)连接AD,BD,
∵AB为⊙O直径,
∴AE⊥BE,
∵∠F=45°,
∴∠EHF=45°,
∴∠BHM=∠EHF=45°,
∵AB⊥CD,
∴∠EBA=45°,
∴∠EAB=45°,
∴∠ADE=∠ABE=∠EAB=45°,
∵BM=MN,
∴CD垂直平分BN,
∴BD=ND,
∴∠DBN=∠DNB,
∴∠AED=∠ABD=∠ANE=∠BND,
∵∠EAB=∠ADE=45°,
∠AEN=∠AED,
∴△AEN∽△ADE,
∴∠ANE=∠DAE,
∴∠DAE=∠AED,
∴AD=DE;
(3)由(2)知,△ABE,△EFH,△BNH是等腰直角三角形,
∵MN=1,
∴BN=2,BH=$\sqrt{2}$,
设AB=2R,
∴AE=BE=$\sqrt{2}$R,
∵∠AEN=∠ANE,
∴AN=AE=$\sqrt{2}$R,
∴$\sqrt{2}$R+2=2R,
∴R=2+$\sqrt{2}$,
∴BE=2$\sqrt{2}$+2,
∴EF=EH=BE-BH=2+$\sqrt{2}$,
∵∠AED=∠FEC,
∵∠FCE=∠EAD,
∴∠FEC=∠FCE,
∴CF=EF=2+$\sqrt{2}$.
点评 本题考查了垂径定理,圆周角定理,等腰三角形的判定和性质,等腰直角三角形的判定和性质,线段垂直平分线的性质,证得△ABE,△EFH,△BNH是等腰直角三角形是解题的关键.

| A. | 9 | B. | 7 | C. | 6.4 | D. | -2 |
 如图,滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
如图,滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则滑雪道的坡顶到坡底的竖直高度AB的长为( )| A. | $\frac{100}{cos20°}$ | B. | $\frac{100}{sin20°}$ | C. | 1OOcos20° | D. | 100sin20° |
| A. | (2,-1) | B. | (-2,-1) | C. | (-1,2) | D. | (1,-2) |
 如图是一个几何体的实物图,则其侧视图是( )
如图是一个几何体的实物图,则其侧视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | 6,4 | B. | -8,14 | C. | -6,6 | D. | -8,-14 |
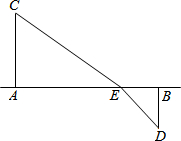 如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时
如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时