题目内容
20.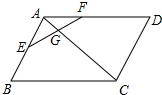 如图,在?ABCD中,E是AB的中点,在AD上截取AF=$\frac{1}{2}$FD,EF交AC于点G,求$\frac{AG}{AC}$的值.
如图,在?ABCD中,E是AB的中点,在AD上截取AF=$\frac{1}{2}$FD,EF交AC于点G,求$\frac{AG}{AC}$的值.
分析 延长FE交CB的延长线于H,如图所示,再由平行线分线段成比例即可证明结论.
解答  解:在?ABCD中,
解:在?ABCD中,
∵AD∥BC,AD=BC,
∴∠AFE=∠H,
在△AEF与△BHE中,
$\left\{\begin{array}{l}{∠AFE=∠H}\\{∠AEF=∠BEH}\\{AE=BE}\end{array}\right.$,
∴△AEF≌△BHE,
∴AF=BH,
∵AF=$\frac{1}{2}$FD,
∴AF=$\frac{1}{3}$AD=$\frac{1}{3}$BC,
∴AF=BH=$\frac{1}{4}$CH,
∵AD∥BC,
∴△AFG∽△CHG,
∴$\frac{AF}{CH}=\frac{AG}{CG}$=$\frac{1}{4}$,
∴$\frac{AG}{AC}$=$\frac{1}{5}$.
点评 本题主要考查了平行四边形的性质,相似三角形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
10.生括中的“对称美”比比皆是,人们把闹钟和飞机制造成对称形状,不仅为了美观,而且还有一定的科学道理:闹钟的对称保证了指针走时的均匀性,飞机的对称能使飞机在空中飞行时保持平衡.下列说法正确的是( )
| A. | 三叶电扇是轴对称图形 | B. | 飞机的两个翅膀是全等形 | ||
| C. | 三角形是轴对称图形 | D. | 圆不是轴对称图形 |
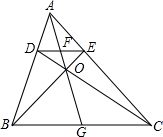 如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明:
如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明: