题目内容
13.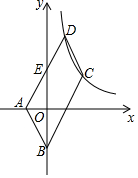 如图,平行四边形ABCD中,A(-1,0),B(0,-2),顶点C、D在双曲线y=$\frac{k}{x}$(x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=4.
如图,平行四边形ABCD中,A(-1,0),B(0,-2),顶点C、D在双曲线y=$\frac{k}{x}$(x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=4.
分析 设点D的坐标为(m,n),根据平行四边形的性质结合点A、B、D的坐标即可得出点C的坐标为(m+1,n-2),由点E为线段AD的中点可得出m=-1,再根据反比例函数图象上点的坐标特征即可得出k=n=2(n-2),解之即可得出k值.
解答 解:设点D的坐标为(m,n),则点C的坐标为(m+1,n-2),
∵边AD交y轴于点E,点E恰好是AD的中点,
∴m=1.
∵k=mn=(m+1)(n-2),即k=n=2(n-2),
解得:n=k=4.
故答案为:4.
点评 本题考查了反比例函数图象上点的坐标特征以及平行四边形的性质,根据反比例函数图象上点的坐标特征找出k=n=2(n-2)是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
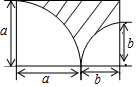 在如图所示的长方形中,请用含字母a,b的代数式表示阴影面积,并按字母a降幂排列得(1-$\frac{1}{4}$π)a2+ab-$\frac{1}{4}$πb2.
在如图所示的长方形中,请用含字母a,b的代数式表示阴影面积,并按字母a降幂排列得(1-$\frac{1}{4}$π)a2+ab-$\frac{1}{4}$πb2.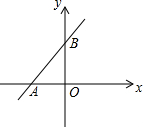 如图,直线y=5x+10与x轴、y轴交于点A,B,则△AOB的面积为10.
如图,直线y=5x+10与x轴、y轴交于点A,B,则△AOB的面积为10.