题目内容
已知AD是△ABC的角平分线，DE⊥AB于E，且DE=3cm，则点D到AC的距离是
- A.2cm
- B.3cm
- C.4cm
- D.6cm
B
分析：如图，过点D作DF⊥AC于点F．利用角平分线的性质可以推知DE=DF=3cm．
解答：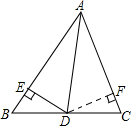
解：如图，过点D作DF⊥AC于点F．
∵AD是△ABC的角平分线，DE⊥AB，
∴DE=DF．
又∵DE=3cm，
∴DF=3cm，即点D到AC的距离是3cm．
故选B．
点评：本题主要考查平分线的性质，即角的平分线上的点到角的两边的距离相等．
分析：如图，过点D作DF⊥AC于点F．利用角平分线的性质可以推知DE=DF=3cm．
解答：
解：如图，过点D作DF⊥AC于点F．∵AD是△ABC的角平分线，DE⊥AB，
∴DE=DF．
又∵DE=3cm，
∴DF=3cm，即点D到AC的距离是3cm．
故选B．
点评：本题主要考查平分线的性质，即角的平分线上的点到角的两边的距离相等．
练习册系列答案
相关题目
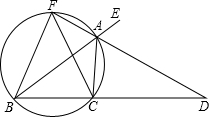于点F，连接FB、FC．
3、如图，已知AD是△ABC的中线，AE=EF=FC，下面给出三个关系式：①AG：AD=1：2；②GE：BE=1：4；③GE：BE=3：4，其中正确的为（ ）
