题目内容
8.(1)计算:-24-$\sqrt{12}$+|1-4sin60°|+(π-$\frac{2}{3}$)0;(2)先化简,再求值:(1-$\frac{3}{x+2}$)÷$\frac{x-1}{{x}^{2}+2x}$-$\frac{x}{x+1}$,其中x满足x2-x-1=0.
分析 (1)原式第一项利用乘方的意义化简,第二项化为最简二次根式,第三项利用绝对值的代数意义化简,最后一项利用零指数幂法则计算即可得到结果;
(2)由已知方程得到x2=x+1,然后代入化简后的代数式进行求值.
解答 解:(1)原式=-16-2$\sqrt{3}$+|1-4×$\frac{\sqrt{3}}{2}$|+1
=-16-2$\sqrt{3}$+2$\sqrt{3}$-1+1
=-16;
(2)∵x2-x-1=0,
∴x2=x+1,
(1-$\frac{3}{x+2}$)÷$\frac{x-1}{{x}^{2}+2x}$-$\frac{x}{x+1}$,
=$\frac{x+2-3}{x+2}$×$\frac{x(x+2)}{x-1}$-$\frac{x}{x+1}$,
=x-$\frac{x}{x+1}$,
=$\frac{{x}^{2}+x-x}{x+1}$
=$\frac{{x}^{2}}{x+1}$,
=$\frac{x+1}{x+1}$
=1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
3. 如图,不能判定AB∥CD的是( )
如图,不能判定AB∥CD的是( )
 如图,不能判定AB∥CD的是( )
如图,不能判定AB∥CD的是( )| A. | ∠2=∠3 | B. | ∠1=∠4 | C. | ∠1=∠2 | D. | ∠1=∠3 |
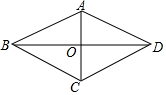 如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O. 如图,已知a∥b,三角板的直角顶点在直线b上.若∠1=40°,则∠2=130度.
如图,已知a∥b,三角板的直角顶点在直线b上.若∠1=40°,则∠2=130度.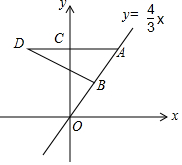 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.