Question

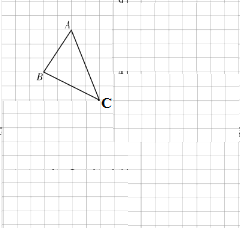
【题目】已知，在边长为1的小正方形组成的网格中，点．

（1）在网格中正确画出平面直角坐标系；

（2）在平面直角坐标系中作出关于轴对称的图形，并将点先向右平移4个单位长度再向下平移1个单位长度得到点，写出点的坐标；

（3）顺次连接点得到，是等腰直角三角形吗？请说明理由．

Answer 1

【答案】（1）详见解析；（2）图详见解析，点的坐标为；（3）是等腰直角三角形，理由详见解析．

【解析】

（1）根据所给的已知点的坐标画直角坐标系；

（2）直接利用关于轴对称点的性质得出对应点位置进而得出答案，再利用平移的性质求得点的坐标；

（3）分别计算出三边的长，根据勾股定理的逆定理进行判断即可．

（1）所建立直角坐标系如下所示：

（2）如上图所示，

观察图象，点的坐标为，

点关于轴对称的点的坐标为，

将点先向右平移4个单位长度再向下平移1个单位长度得到点，

∴点的横坐标为：，纵坐标为：，

∴点的坐标为；

（3）是等腰直角三角形．

∵点、、的坐标分别为、、

∴，

，

，

∴，

∴是等腰直角三角形．