题目内容
已知△AOB在平面直角坐标系中,A(1,3),B(2,0),经过点C(-2,0)的一条直线交线段AO于点D,交线段AB于点E,S△COD=S△ADE.
(1)求直线CD的表达式;
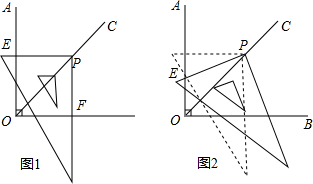
(2)若直线CD交y轴于点F,在平面内是否存在一点P,使△FOC≌△FOP?若存在,求出点P的坐标.
(1)求直线CD的表达式;
(2)若直线CD交y轴于点F,在平面内是否存在一点P,使△FOC≌△FOP?若存在,求出点P的坐标.
考点:一次函数综合题
专题:
分析:(1)设直线CD解析式为y=kx+b,分别求得点D,E的纵坐标,根据S△COD=S△ADE即可解题;
(2)在图中画出点P存在的位置,使得△FOC≌△FOP,根据数形结合的方式解本题.
(2)在图中画出点P存在的位置,使得△FOC≌△FOP,根据数形结合的方式解本题.
解答:解:(1)过A,D,E作AH⊥OB,DM⊥OB,EN⊥OB,
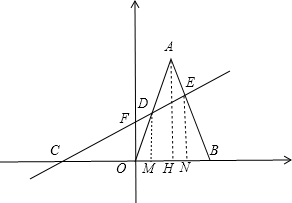
设直线CD解析式为y=kx+b,代入C点得,b=2k,
∴直线CD解析式为y=kx+2k,
∵直线AB的解析式为y=-3x+6,直线OA的解析式为y=3x,
∴D点纵坐标为
,E点纵坐标为
,
∵△ADE面积=△ABO面积-四边形DEBO的面积,
四边形DEBO的面积=△EBC面积-△COD面积;
∴
×2×3-(
×4×
-
×2×
)=
×2×
解得:k=
,
∴直线CD解析式为y=
x+
.
(2)直线CD与y轴交点为:当x=0时,y=
,
则点F坐标为(0,
),
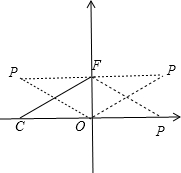
从图中可以看出当P纵坐标为
,横坐标为2或-2时,△FOC≌△FOP,
或者P与D点重合时,△FOC≌△FOP,
故存在点P,点P坐标为(2,0)或(2,
)或(-2,
).

设直线CD解析式为y=kx+b,代入C点得,b=2k,
∴直线CD解析式为y=kx+2k,
∵直线AB的解析式为y=-3x+6,直线OA的解析式为y=3x,
∴D点纵坐标为
| 6k |
| k-3 |
| 12k |
| k+3 |
∵△ADE面积=△ABO面积-四边形DEBO的面积,
四边形DEBO的面积=△EBC面积-△COD面积;
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 12k |
| k+3 |
| 1 |
| 2 |
| 6k |
| k-3 |
| 1 |
| 2 |
| 6k |
| k-3 |
解得:k=
| 3 |
| 7 |
∴直线CD解析式为y=
| 3 |
| 7 |
| 6 |
| 7 |
(2)直线CD与y轴交点为:当x=0时,y=
| 6 |
| 7 |
则点F坐标为(0,
| 6 |
| 7 |

从图中可以看出当P纵坐标为
| 6 |
| 7 |
或者P与D点重合时,△FOC≌△FOP,
故存在点P,点P坐标为(2,0)或(2,
| 6 |
| 7 |
| 6 |
| 7 |
点评:本题考查了直线交点坐标的求解,考查了一次函数的求解问题,考查了数形结合解题的方法,本题中求得k的值是解题的关键.

练习册系列答案
相关题目
下列方程中,不能用直接开平方法的是( )
| A、x2-3=0 |
| B、(x-1)2-4=0 |
| C、x2+2x=0 |
| D、(x-1)2=(2x+1)2 |
 如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,
如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,