题目内容
 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,An-1Bn-1=An-1An,∠B=20°,则∠An=
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,An-1Bn-1=An-1An,∠B=20°,则∠An=考点:等腰三角形的性质
专题:规律型
分析:在△ABA1中由三角形内角和定理可求得∠BA1A,结合外角的性质依次可得出∠BA1A=2∠B1A2A1=4∠B2A3A2=…=2n-1∠Bn-1AnAn-1,可求得答案.
解答:解:∵AB=A1B,
∴∠A=∠BA1A,且∠B=20°,
∴∠BA1A=
=80°,
∵A1B1=A1A2,
∴∠BA1A=2∠B1A2A1,
依次可得到∠BA1A=2∠B1A2A1=4∠B2A3A2=…=2n-1∠Bn-1AnAn-1,
即80°=2n-1∠An,
∴∠An=
.
故答案为:
.
∴∠A=∠BA1A,且∠B=20°,
∴∠BA1A=
| 180°-20° |
| 2 |
∵A1B1=A1A2,
∴∠BA1A=2∠B1A2A1,
依次可得到∠BA1A=2∠B1A2A1=4∠B2A3A2=…=2n-1∠Bn-1AnAn-1,
即80°=2n-1∠An,
∴∠An=
| 80° |
| 2n-1 |
故答案为:
| 80° |
| 2n-1 |
点评:本题主要考查等腰三角形的性质及外角的性质,利用等边对等角和外角等于不相邻两个内角的和得到∠BA1A=2n-1∠Bn-1AnAn-1是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
规定以下两种变换:①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n),如g(2,1)=(-2,-1).按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(-2,3)]等于( )
| A、(-2,-3) |
| B、(2,-3) |
| C、(-2,3) |
| D、(2,3) |
 实数a,b在数轴上的位置如图所示,则化简|b-a|+|a|+|b|的结果为( )
实数a,b在数轴上的位置如图所示,则化简|b-a|+|a|+|b|的结果为( )| A、2a | B、2b |
| C、2b-2a | D、0 |
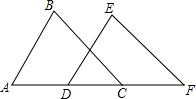 如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.
如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.