äãá¢áÖàï
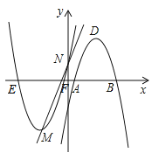
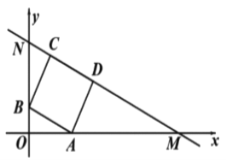
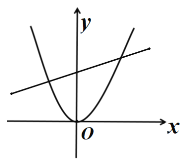
Àƒäãá¢À¢àÓë¥È˜éæöÿüÔy=ax2+(4aˋ1)xˋ4ÆŠxøç£ÆÖçÐAÀÂBȘƊyøç£ÆÖçÐCȘúØOC=2OBȘçÐDöˆüÔÑöOBèüØ£Ñ₤çÐ(ý£ÆŠçÐBøĤü)Ș¿»çÐD漃ÄÅöDEFHȘçÐHÀÂFåÖéæöÿüÔèüȘçÐEåÖxøÃèüÈÛ
È´1ÈˋúµéæöÿüÔçá§ãö—ò§È£
È´2Èˋç݃ÄÅöDEFHçáøÉ°ÊæŸÇµòÝȘúµƒÄÅöDEFHçáûÌ£»È£
È´3ÈˋåÖÈ´2Èˋçáä¾¥±üôȘƒÄÅöDEFHý£Ñ₤Ș§¨éæöÿüÔîÄæéxøÃü·æµó§Øóm¡—çËö£È˜éæöÿüÔÆŠƒÄÅöDEFHçáÝÔ§£ÆÖçÐMÀÂNȘ꘧ÆMÀÂNÈÛà¶MNúÀ¤ûó§ñøƒÄÅöDEFHçáûÌ£»È˜úµmçáøçÈÛ
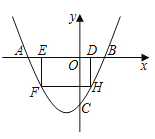
ÀƒÇÞ¯¡À¢È´1Èˋy=![]() x2+xˋ4ȣȴ2Èˋ10ȣȴ3Èˋmçáøçöˆ
x2+xˋ4ȣȴ2Èˋ10ȣȴ3Èˋmçáøçöˆ![]() ÈÛ
ÈÛ
Àƒ§ãö—À¢
È´1Èˋüàúµ°—çÐCçáæ½ÝõȘÆèOCȧ2OBȘ¢èëó°—çÐBæ½ÝõȘ§¨çÐBæ½ÝõǺàŠyȧax2Ȩȴ4aˋ1Èˋxˋ4¢èúµ°—açáøçȘ¥Ç¢èÅÇ°—éæöÿüÔçá§ãö—ò§È£
È´2ÈˋèÒçÐDæ½ÝõöˆÈ´xȘ0ÈˋȘÆû¤˜xçáǺò»ò§ÝÚòƒ°—ƒÄÅöDEFHçáøÉ°ÊȘÆû¤₤ò»çáù¥üŠúµ°—àÀóðæŸÇµøçòÝxçáøçȘ¥Çúµ°—çÐDçáæ½ÝõȘ§½Ø£ý§¢èúµ°—ƒÄÅöDEFHçáûÌ£»È£
È´3ÈˋàÓë¥È˜ê˜§ÆBHȘEHȘDFȘèÒEHÆŠDF§£ÆÖçÐGȘ¿»çÐGæ¼BHçáó§ÅÅüÔȘ§£EDÆÖMȘ§£HFÆÖçÐNȘå·øÝüÔMN§¨ƒÄÅöDEFHçáûÌ£»ñø°èüÁçàçáꧯŠÈ˜ØâÇöúµ°—øÝüÔBHȘMNçá§ãö—ò§È˜åìúµ°—çÐMçáæ½ÝõȘ¥Ç¢èçû°—mçáøçÈÛ
§ãȤȴ1ÈˋåÖéæöÿüÔyȧax2Ȩ(4aˋ1)xˋ4øÅȘ
çÝxȧ0òÝȘyȧˋ4Ș
ÀÁC(0Șˋ4)Ș
ÀÁOCȧ4ÈÛ
ÀÔOCȧ2OBȘ
ÀÁOBȧ2Ș
ÀÁB(2Ș0)Ș
§¨B(2Ș0)ǺàŠyȧax2Ȩ(4aˋ1)xˋ4ȘçûȤaȧ![]() Ș
Ș
ÀÁéæöÿüÔçá§ãö—ò§öˆyȧ![]() x2Ȩxˋ4È£
x2Ȩxˋ4È£
È´2ÈˋèÒçÐDæ½Ýõöˆ(xȘ0)ÈÛ
ÀÔùáÝÔÅöDEFHöˆƒÄÅöȘ
ÀÁH(xȘ![]() x2Ȩxˋ4)ÈÛ
x2Ȩxˋ4)ÈÛ
ÀÔyȧ![]() x2Ȩxˋ4ȧ
x2Ȩxˋ4ȧ![]() (xȨ1)2ˋ
(xȨ1)2ˋ![]() Ș
Ș
ÀÁéæöÿüÔÑå°óøÃöˆxȧˋ1Ș
ÀÁçÐHç§Ñå°óøÃçáƒÁâŠöˆxȨ1Ș
ÆèÑå°óÅå¢èøˆDEȧFHȧ2xȨ2Ș
ÀÁƒÄÅöDEFHçáøÉ°ÊCȧ2(2xȨ2)Ȩ2(ˋ![]() x2ˋxȨ4)ȧˋx2Ȩ2xȨ12ȧˋ(xˋ1)2Ȩ13Ș
x2ˋxȨ4)ȧˋx2Ȩ2xȨ12ȧˋ(xˋ1)2Ȩ13Ș
ÀÁçÝxȧ1òÝȘƒÄÅöDEFHøÉ°ÊàÀæŸÇµøç13Ș
ÀÁÇùòÝH(1Șˋ![]() )Ș
)Ș
ÀÁHFȧ2xȨ2ȧ4ȘDHȧ![]() Ș
Ș
ÀÁSƒÄÅöDEFHȧHFDH![]() ȧ10È£
ȧ10ȣ
È´3ÈˋàÓë¥È˜
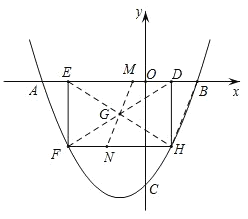
꘧ÆBHȘEHȘDFȘèÒEHÆŠDF§£ÆÖçÐGȘ
¿»çÐGæ¼BHçáó§ÅÅüÔȘ§£EDÆÖMȘ§£HFÆÖçÐNȘå·øÝüÔMN§¨ƒÄÅöDEFHçáûÌ£»ñø°èüÁçàçáꧯŠÈ˜
ÆèÈ´2ÈˋøˆÈ˜éæöÿüÔÑå°óøÃöˆxȧˋ1ȘH(1Șˋ![]() )Ș
)Ș
ÀÁG(ˋ1Șˋ![]() )Ș
)Ș
èÒøÝüÔBHçá§ãö—ò§öˆyȧkxȨbȘ
§¨çÐB(2Ș0)ȘH(1Șˋ![]() )ǺàŠÈ˜
)ǺàŠÈ˜
çûȤ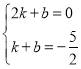 Ș§ãçûȤ
Ș§ãçûȤ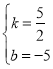 Ș
Ș
ÀÁøÝüÔBHçá§ãö—ò§öˆyȧ![]() xˋ5Ș
xˋ5Ș
ÀÁ¢èèÒøÝüÔMNçá§ãö—ò§öˆyȧ![]() xȨnȘ
xȨnȘ
§¨çÐ(ˋ1Șˋ![]() )ǺàŠÈ˜çûnȧ
)ǺàŠÈ˜çûnȧ![]() Ș
Ș
ÀÁøÝüÔMNçá§ãö—ò§öˆyȧ![]() xȨ
xȨ![]() Ș
Ș
çÝyȧ0òÝȘxȧˋ![]() Ș
Ș
ÀÁM(ˋ![]() Ș0)ÈÛ
Ș0)ÈÛ
ÀÔB(2Ș0)Ș
ÀÁ§¨éæöÿüÔîÄæéxøÃü·æµó§Øó![]() ¡—çËö£È˜éæöÿüÔÆŠƒÄÅöDEFHçáÝÔ§£ÆÖçÐMÀÂNȘ
¡—çËö£È˜éæöÿüÔÆŠƒÄÅöDEFHçáÝÔ§£ÆÖçÐMÀÂNȘ
꘧ÆMÀÂNȘå·MNúÀ¤ûó§ñøƒÄÅöDEFHçáûÌ£»È˜
ÀÁmçáøçöˆ![]() ÈÛ
ÈÛ

 òŸ¥ìæ¼ØçòŸ¥ì¢šâøêñö¼¯ý°—¯ÌèÓüçêÅÇÞ¯¡
òŸ¥ìæ¼ØçòŸ¥ì¢šâøêñö¼¯ý°—¯ÌèÓüçêÅÇÞ¯¡Àƒäãá¢À¢àÓë¥È˜åÖäïÅö![]() øÅȘ
øÅȘ![]() Ș
Ș![]() Ș
Ș![]() Ș
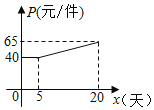
Ș![]() ÈÛPöˆüÔÑö
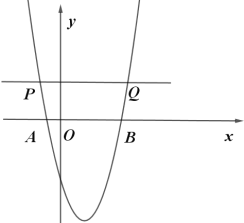
ÈÛPöˆüÔÑö![]() èüçáØ£Ñ₤çÐȘúؤëBÀÂCý£øĤüȘ꘧Æ
èüçáØ£Ñ₤çÐȘúؤëBÀÂCý£øĤüȘ꘧Æ![]() Ș¿»çÐPæ¼
Ș¿»çÐPæ¼![]() §£èðüÔ
§£èðüÔ![]() ÆÖçÐEÈÛ
ÆÖçÐEÈÛ
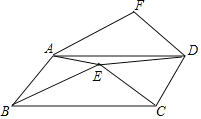
ÇüÇü¡ªƒïîÏü¯¤₤ò»çáƒÙîÕȘÑåíã¡—öòä㧽ÅÅêùîŃ¢È¤
È´1Èˋë´¿»ëóâÚȘù«ñÂüø![]() ȘúŠáЯÿù«ëõ°èøÊû¼ÈÛ
ȘúŠáЯÿù«ëõ°èøÊû¼ÈÛ
È´2Èˋâ«Æû¥¡¤ö£Ù¯ÍȘù«¡áÝð![]() çá°ÊÑàȘåùÑ₤çÐPȘçûç§ý£ë˜ö£øûòÝȘ
çá°ÊÑàȘåùÑ₤çÐPȘçûç§ý£ë˜ö£øûòÝȘ![]() ÀÂ
ÀÂ![]() çá°ÊÑàçáÑåÆÎøçȤ
çá°ÊÑàçáÑåÆÎøçȤ
çÝ![]() òÝȘçûÝÚ1Ȥ
òÝȘçûÝÚ1Ȥ
| ÀÙ | 1 | 2 | 3 | 4 | 5 | ÀÙ |
| ÀÙ | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | ÀÙ |
çÝ![]() òÝȘçûÝÚ2Ȥ
òÝȘçûÝÚ2Ȥ
| ÀÙ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ÀÙ |
| ÀÙ | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | ÀÙ |
íãùçû¼È˜çÐPåÖüÔÑö![]() èüåùÑ₤òÝȘ؈ÝÈøÊçÐEæÉåÖüÔÑö
èüåùÑ₤òÝȘ؈ÝÈøÊçÐEæÉåÖüÔÑö![]() èüȘ
èüȘ![]() çá°ÊÑàÆÎÆÅأѴçáüßøóÈÛ
çá°ÊÑàÆÎÆÅأѴçáüßøóÈÛ
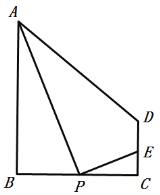
Âì䟢íȤ¡ªƒï¤₤ò»çáÑ´ØÍȘöØûú¢èØåàñѴȘåÖ![]() ¤ë
¤ë![]() çá°ÊÑàíãꧡ—Ýðê¢øÅȘ_____çá°ÊÑàöˆæåÝðê¢È˜_____çá°ÊÑàöˆØ·Ýðê¢È£
çá°ÊÑàíãꧡ—Ýðê¢øÅȘ_____çá°ÊÑàöˆæåÝðê¢È˜_____çá°ÊÑàöˆØ·Ýðê¢È£
ÂÖèÒ![]() ȘçÝçÐPåÖüÔÑö
ȘçÝçÐPåÖüÔÑö![]() èüåùÑ₤òÝȘçÐEæÉåÖüÔÑö
èüåùÑ₤òÝȘçÐEæÉåÖüÔÑö![]() èüȘúµmçáàÀøçñÑöÏÈÛ
èüȘúµmçáàÀøçñÑöÏÈÛ