题目内容
【题目】已知数轴上三点![]() 、
、![]() 、
、![]() 表示的数分别为4、0、
表示的数分别为4、0、![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒3个单位的速度沿数轴向左匀速运动.
点出发,以每秒3个单位的速度沿数轴向左匀速运动.
(1)当点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等时,点
的距离相等时,点![]() 在数轴上表示的数是 .
在数轴上表示的数是 .
(2)另一动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿数轴向左匀速运动,若点
出发,以每秒2个单位的速度沿数轴向左匀速运动,若点![]() 、
、![]() 同时出发,问点
同时出发,问点![]() 运动多长时间追上点
运动多长时间追上点![]() ?
?
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段
的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段![]() 的长度.
的长度.

【答案】(1)1;(2)6秒;(3) MN的长度不变,为3
【解析】
(1)根据题意可得点P为AB的中点,然后根据数轴上中点公式即可求出结论;
(2)先求出AB的长,设![]() 点运动
点运动![]() 秒追上
秒追上![]() 点,根据题意,列出方程即可求出结论;
点,根据题意,列出方程即可求出结论;
(3)根据点P在线段AB上和点P在AB的延长线上分类讨论,分别画出对应的图形,根据中点的定义即可求出结论.
解:(1)∵点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等
的距离相等
∴点P为AB的中点
∴点![]() 在数轴上表示的数是
在数轴上表示的数是![]()
故答案为:1;
(2)AB=4-(-2)=6
设![]() 点运动
点运动![]() 秒追上
秒追上![]() 点,由题意得:
点,由题意得:
![]()
解得:![]()
答:![]() 点运动6秒追上
点运动6秒追上![]() 点.
点.
(3)![]() 的长度不变.
的长度不变.
①当![]() 点在线段
点在线段![]() 上时,如图示:
上时,如图示:

∵![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点
的中点
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
②当![]() 点在线段
点在线段![]() 的延长线上时,如图示:
的延长线上时,如图示:
![]()
∵![]()
∴![]()
![]()
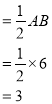

练习册系列答案
相关题目