题目内容
 如图,圆锥的底面半径为1,母线长为3,则这个圆锥的侧面积是
如图,圆锥的底面半径为1,母线长为3,则这个圆锥的侧面积是
- A.π
- B.2π
- C.3π
- D.4π
C
分析:根据圆锥的侧面展开扇形的弧长等于圆锥底面周长,先求出弧长,然后用弧长与母线长乘积的一半求侧面展开扇形的面积.
解答:圆锥的底面周长为:2πr=2π×1=2π,
∴圆锥的侧面展开扇形的弧长为:2π,
∴其面积为: lr=
lr= ×2π×3=3π,
×2π×3=3π,
故选C.
点评:本题考查了圆锥侧面展开扇形的面积的计算方法,解决本题的关键是正确的将侧面展开扇形的弧长转化为圆锥的底面周长.
分析:根据圆锥的侧面展开扇形的弧长等于圆锥底面周长,先求出弧长,然后用弧长与母线长乘积的一半求侧面展开扇形的面积.
解答:圆锥的底面周长为:2πr=2π×1=2π,
∴圆锥的侧面展开扇形的弧长为:2π,
∴其面积为:
 lr=
lr= ×2π×3=3π,
×2π×3=3π,故选C.
点评:本题考查了圆锥侧面展开扇形的面积的计算方法,解决本题的关键是正确的将侧面展开扇形的弧长转化为圆锥的底面周长.

练习册系列答案
相关题目
 如图,圆锥的底面半径为1,侧面积为3π,则这个圆锥的母线长是( )
如图,圆锥的底面半径为1,侧面积为3π,则这个圆锥的母线长是( )| A、0.5 | B、1 | C、2 | D、3 |
 如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是( )
如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是( )| A、10πcm2 | B、15πcm2 | C、20πcm2 | D、25πcm2 |
 如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )
如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )| A、8 | ||
B、10
| ||
C、15
| ||
D、20
|
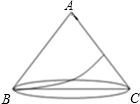 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少? (2013•增城市二模)如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )
(2013•增城市二模)如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )