题目内容
7．
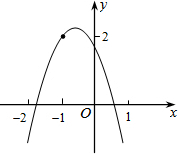如图所示，二次函数 y=ax2+bx+c （a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，下列结论（1）4a-2b+c＜0；（2）2a-b＜0；（3）a-3b＞0；（4）b2+8a＜4ac； 其中正确的有（1），（2），（3）．
分析 由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解答 
解：（1）根据图象知，当x=-2时，y＜0，即4a-2b+c＜0；故本选项正确；
（2）∵该函数图象的开口向下，∴a＜0；
又对称轴-1＜x=-$\frac{b}{2a}$＜0，∴2a-b＜0，故本选项正确；
（3）∵a＜0，-$\frac{b}{2a}$＜0，
∴b＜0，
∵二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），
∴a-b+c=2，
∵0＜c＜2，
∴a-b=2-c＞0，
则a-3b＞0．
故本选项正确；
（4）∵y=$\frac{4ac-{b}^{2}}{4a}$＞2，a＜0，
∴4ac-b2＜8a，即b2+8a＞4ac，故本选项错误．
综上所述，正确的结论有3个；
故答案为：（1），（2），（3）．
点评 本题主要考查对二次函数图象与系数的关系，抛物线与x轴的交点，二次函数图象上点的坐标特征等知识点的理解和掌握．二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．
练习册系列答案
相关题目
18．下列说法中，正确的是（ ）
| A． | 1的平方根是1 | B． | -1是1的平方根 | C． | 8的立方根是±2 | D． | $\sqrt{9}$=±3 |
如图，已知△ABC（AC＜BC），用尺规在BC上确定一点P，使PA+PC=BC．
2．化简$\frac{{{x^2}-1}}{x-1}$正确的是（ ）
| A． | $\frac{{{x^2}-1}}{x-1}=\frac{{{{（x-1）}^2}}}{x-1}=\frac{1}{x-1}$ | B． | $\frac{{{x^2}-1}}{x-1}=\frac{{{{（x-1）}^2}}}{x-1}=x-1$ | ||
| C． | $\frac{{{x^2}-1}}{x-1}=\frac{（x+1）（x-1）}{x-1}=x+1$ | D． | $\frac{{{x^2}-1}}{x-1}=\frac{（x+1）（x-1）}{x-1}=\frac{1}{x+1}$ |
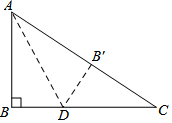如图所示，有一块直角三角形纸片，两直角边AB=6，BC=8，将三角形ABC折叠，使AB落在斜边AC上得到线段AB'，折痕为AD，则BD的长为3．
17．$\frac{1}{2}$是一个数的算术平方根，则这个数为（ ）
| A． | 4 | B． | 1 | C． | $\frac{1}{4}$ | D． | ±$\frac{1}{4}$ |