题目内容
18.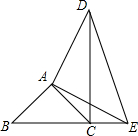 如图,已知∠BAC=∠DAE=90°,AB=AC,AD=AE,点B、C、E在同一条直线上,求证:DC⊥BE.
如图,已知∠BAC=∠DAE=90°,AB=AC,AD=AE,点B、C、E在同一条直线上,求证:DC⊥BE.
分析 根据已知证明△BAE≌△CAD(SAS),所以∠ACD=∠ABC=45°,得到∠ACB+∠ACD=90°,即DC⊥BE.
解答 解:∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,∠ABC=∠ACB=45°,
∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD,
在△BAE和△CAD中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AD=AE}\end{array}\right.$
∴△BAE≌△CAD(SAS)
∴∠ACD=∠ABC=45°,
∴∠ACB+∠ACD=90°.
即DC⊥BE.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△BAE≌△CAD.

练习册系列答案
相关题目
9.下列命题是假命题的是( )
| A. | 对顶角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 同角的余角相等 | D. | 两个锐角的和等于直角 |
6.等腰三角形的周长为16,其中一边长为6,则另两边长为( )
| A. | 6和4 | B. | 5和5 | C. | 6和6 | D. | 6和4或5和5 |
3.据统计,2014年3月(共31天)北京市空气质量等级天数如下表所示:
(1)请根据所给信息补全统计表;
(2)市环保局正式发布了北京PM2.5来源的最新研究成果,专家通过论证已经分析出汽车尾气排放是本地主要污染源.在北京市小客车数量调控方案中,将逐年增加新能源小客车的指标.已知2014年的指标为2万辆,计划2016年的指标为6万辆,假设2014~2016年新能源小客车指标的年增长率相同且均为x,求这个年增长率x.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449)
| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 5 | 11 | 3 | 7 | 2 | 3 |
(2)市环保局正式发布了北京PM2.5来源的最新研究成果,专家通过论证已经分析出汽车尾气排放是本地主要污染源.在北京市小客车数量调控方案中,将逐年增加新能源小客车的指标.已知2014年的指标为2万辆,计划2016年的指标为6万辆,假设2014~2016年新能源小客车指标的年增长率相同且均为x,求这个年增长率x.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449)
8.若|a|=-a,则a是( )
| A. | 非负数 | B. | 负数 | C. | 正数 | D. | 非正数 |
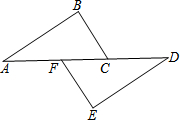 已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.