题目内容
已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为
 ,则⊙O的半径为 .
,则⊙O的半径为 .


4 .
【考点】正多边形和圆.
【分析】要求三角形的面积就要先求出它的边长,根据正多边形与圆的关系即可求出.
【解答】解:阴影部分是一个正三角形,连接DO并延长,交BF于点G.
设边长是a,
则面积是
 ,
,
得到
 =12
=12
 ,
,
解得a=4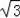
 ,
,
则DG=BD•sin60°=4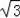
 ×
×
 =6
=6
因而半径OD=
 DG=6×
DG=6×
 =4.
=4.


【点评】本题主要考查了正多边形的计算,是一个基础题.

练习册系列答案
相关题目

 ,则AB的长是 .
,则AB的长是 .



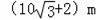
 B.
B.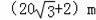

 D.
D.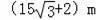
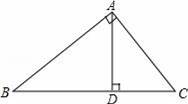


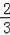
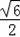
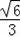
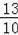
 ,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.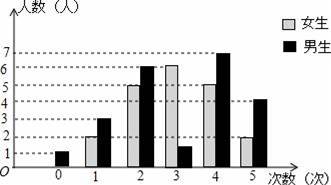




 的解集是 .
的解集是 .